
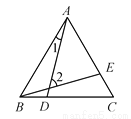
如图所示,△ABC是等边三角形,且BD=CE,∠1=15°,则∠2的度数为( )
A. 15° B. 30° C. 45° D. 60°
D 【解析】因为△ABC是等边三角形,所以∠ABD=∠BCE=60°,AB=BC. 因为BD=CE,所以△ABD≌△BCE,所以∠1=∠CBE. 因为∠CBE+∠ABE=60°,所以∠1+∠ABE=60°. 因为∠2=∠1+∠ABE,所以∠2=60°. 故选D.科目:初中数学 来源:宁夏2017-2018第一学年七年级上册数学期末综合检测模拟试卷 题型:单选题
在下列调查中,适宜采用全面调查的是( )
A. 了解我省中学生的视力情况
B. 了解七(1)班学生校服的尺码情况
C. 检测一批电灯泡的使用寿命
D. 调查安徽卫视《超级演说家》栏目的收视率
B 【解析】试题分析:由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似. 【解析】 A、了解我省中学生的视力情况,调查范围广,适合抽样调查,故A错误; B、了解七(1)班学生校服的尺码情况,适合普查,故B正确; C、检测一批电灯泡的使用寿命,调查具有破坏性,适合抽样调查,故C错误; D、调查安徽卫视《第一时间》栏目的收视率,...查看答案和解析>>
科目:初中数学 来源:山东省潍坊市诸城市2016-2017学年八年级(上)期末数学试卷 题型:填空题
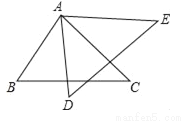
已知△ABC≌△ADE,如果∠BAE=135°,∠BAD=40°,那么∠BAC=______.
查看答案和解析>>
科目:初中数学 来源:安徽省合肥市2016~17学年度第一学期 期末教学质量检测 八年级数学试卷 题型:解答题
一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,求原多边形的边数.
7、8或9. 【解析】试题分析:根据切后的内角和可以求出切后的多边形边数,然后又知一个多边形切去一个角可得到的多边形有三种可能,分别是比原边数少1,相等,多1.所以可求得原多边形边数. 设切去一角后的多边形为n边形. 根据题意有(n-2)·180°=1 080°.解得n=8. 因为一个多边形切去一个角后形成的多边形边数有三种可能:比原多边形边数小1、相等、大1, 所以...查看答案和解析>>
科目:初中数学 来源:安徽省合肥市2016~17学年度第一学期 期末教学质量检测 八年级数学试卷 题型:填空题
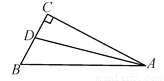
如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=15,且BD∶DC=3∶2,则D到边AB的距离是_________.
查看答案和解析>>
科目:初中数学 来源:安徽省合肥市2016~17学年度第一学期 期末教学质量检测 八年级数学试卷 题型:单选题
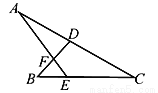
如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于( )
A. 120° B. 115° C. 110° D. 105°
C 【解析】试题分析:因为∠A=27°,∠C=38°,所以∠AEB=∠A+∠C=65°,又因∠B=45°,所以∠DFE=∠B+∠AEB=110°,故选C.查看答案和解析>>
科目:初中数学 来源:吉林省2017-2018学年度七年级数学上册期末测试卷 题型:解答题
一个角的余角比这个角的 少30°,请你计算出这个角的大小.
少30°,请你计算出这个角的大小.
查看答案和解析>>
科目:初中数学 来源:吉林省2017-2018学年度七年级数学上册期末测试卷 题型:单选题
下列各组单项式中,为同类项的是( )
A. a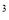 与a
与a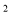 B.
B. 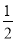 a
a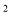 与2a
与2a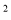 C. 2xy与2x D. -3与a
C. 2xy与2x D. -3与a
查看答案和解析>>
科目:初中数学 来源:甘肃省白银市2018届九年级(上)期中数学试卷 题型:填空题
已知实数m,n满足3m2+6m﹣7=0,3n2+6n﹣7=0,且m≠n,则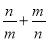 =_____.
=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com