
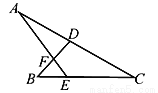
如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于( )
A. 120° B. 115° C. 110° D. 105°
C 【解析】试题分析:因为∠A=27°,∠C=38°,所以∠AEB=∠A+∠C=65°,又因∠B=45°,所以∠DFE=∠B+∠AEB=110°,故选C. 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源:湖北省襄阳市襄城区2016-2017学年度上学期期末考试九年级数学试卷 题型:解答题
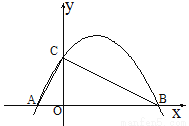
如图,在平面直角坐标系中,抛物线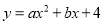 与坐标轴分别交于点A、点B、点C,并且∠ACB=90º,AB=10.
与坐标轴分别交于点A、点B、点C,并且∠ACB=90º,AB=10.
(1)求证:△OAC∽△OCB;
(2)求该抛物线的解析式;
(3)若点P是(2)中抛物线对称轴上的一个动点,是否存在点P使得△PAC为等腰三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:山东省潍坊市诸城市2016-2017学年八年级(上)期末数学试卷 题型:单选题
对于非零的两个实数a,b,规定a⊕b=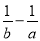 ,若2⊕(2x﹣1)=1,则x的值为( )
,若2⊕(2x﹣1)=1,则x的值为( )
A. 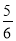 B.
B. 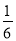 C.
C. 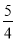 D.
D. 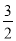
查看答案和解析>>
科目:初中数学 来源:安徽省合肥市2016~17学年度第一学期 期末教学质量检测 八年级数学试卷 题型:填空题
已知x2-2(m+3)x+9是一个完全平方式,则m=____________.
-6或0. 【解析】由题意得-2(m+3)=2, 所以解得m=-6或0.查看答案和解析>>
科目:初中数学 来源:安徽省合肥市2016~17学年度第一学期 期末教学质量检测 八年级数学试卷 题型:单选题
如图所示,△ABC是等边三角形,且BD=CE,∠1=15°,则∠2的度数为( )
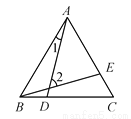
A. 15° B. 30° C. 45° D. 60°
D 【解析】因为△ABC是等边三角形,所以∠ABD=∠BCE=60°,AB=BC. 因为BD=CE,所以△ABD≌△BCE,所以∠1=∠CBE. 因为∠CBE+∠ABE=60°,所以∠1+∠ABE=60°. 因为∠2=∠1+∠ABE,所以∠2=60°. 故选D.查看答案和解析>>
科目:初中数学 来源:吉林省2017-2018学年度七年级数学上册期末测试卷 题型:解答题
解方程: 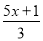 -
-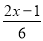 =1.
=1.
查看答案和解析>>
科目:初中数学 来源:吉林省2017-2018学年度七年级数学上册期末测试卷 题型:填空题
青藏高原是世界上海拔最高的高原,它的面积约为2 500 000平方千米.将2 500 000用科学记数法表示应为_________________平方千米.
2.5×106 【解析】试题解析:2500000=2.5.查看答案和解析>>
科目:初中数学 来源:2017-2018学年内蒙古乌兰察布市分校九年级(上)期中数学试卷 题型:解答题
如图,经过点A(0,﹣4)的抛物线y=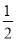 x2+bx+c与x轴相交于点B(﹣1,0)和C,O为坐标原点.
x2+bx+c与x轴相交于点B(﹣1,0)和C,O为坐标原点.
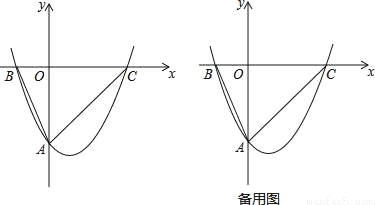
(1)求抛物线的解析式;
(2)将抛物线y=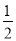 x2+bx+c向上平移7个单位长度,再向左平移m(m>0)个单位长度,得到新抛物线,若新抛物线的顶点P在△ABC内,求m的取值范围;
x2+bx+c向上平移7个单位长度,再向左平移m(m>0)个单位长度,得到新抛物线,若新抛物线的顶点P在△ABC内,求m的取值范围;
(3)将x轴下方的抛物线图象关于x轴对称,得到新的函数图象C,若直线y=x+k与图象C始终有3个交点,求满足条件的k的取值范围.
(1)y=x2﹣x﹣4(2)<m<(3)1或 【解析】试题分析: (1)将A、B两点坐标代入即可解出的值,从而得到抛物线的解析式; (2)将(1)中所得解析式配方,结合已知条件可得平移所得新抛物线的解析式及其顶点坐标;由A、B、C三点的坐标可求得直线AB、AC的解析式,由顶点分别落在AB和AC上可求得对应的“m”的值,即可得到“m”的取值范围; (3)如图1,当直线和新的函...查看答案和解析>>
科目:初中数学 来源:甘肃省白银市2018届九年级(上)期中数学试卷 题型:填空题
已知关于x的一元二次方程ax2﹣2x﹣1=0有两个不相等的实数根,则a的取值范围是__________
a>﹣1且a≠0 【解析】∵关于的一元二次方程有两个不相等的实数根, ∴ ,解得: 且. 即的取值范围是: 且.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com