
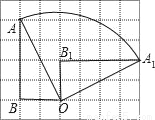
如图,在小正方形的边长都为1的方格纸中,△ABO的顶点都在小正方形的顶点上,将△ABO绕点O顺时针方向旋转90°得到△A1B1O,则点A运动的路径长为_____.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017年天津二十一中中考数学冲刺试卷(2) 题型:单选题
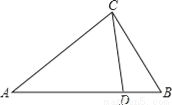
如图,△ACD和△ABC相似需具备的条件是( )
A. 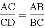 B.
B. 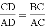 C. AC2=AD•AB D. CD2=AD•BD
C. AC2=AD•AB D. CD2=AD•BD
查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:填空题
芜湖国际动漫节期间,小明进行了富有创意的形象设计.如图1,他在边长为1的正方形ABCD内作等边三角形BCE,并与正方形的对角线交于F、G点,制成如图2的图标.则图标中阴影部分图形AFEGD的面积=_____.
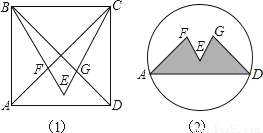
查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:单选题
在实数π、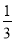 、
、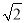 、0.1234中,无理数的个数为( )
、0.1234中,无理数的个数为( )
A. 1 B. 2 C. 3 D. 4
B 【解析】根据无理数的概念,无限不循环小数是无理数,可知π、是无理数. 故选:B.查看答案和解析>>
科目:初中数学 来源:2017年吉林省长春市中考数学模拟试卷(7) 题型:解答题
如图,在?ABCD中,点E,F分别在边AD,BC上,点M,N在对角线AC上,且AE=CF,AM=CN,求证:四边形EMFN是平行四边形.
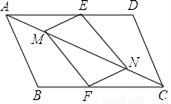
查看答案和解析>>
科目:初中数学 来源:2017年吉林省长春市中考数学模拟试卷(7) 题型:单选题
如图,在平面直角坐标系中,点A,B分别在x轴、y轴的正半轴上,OA=6,OB=9,点C在函数y=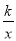 (x>0)的图象上,当点C的横坐标为4时,△OAC与△OBC的面积相等,k的值为( )
(x>0)的图象上,当点C的横坐标为4时,△OAC与△OBC的面积相等,k的值为( )
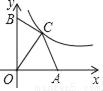
A. 16 B. 24 C. 30 D. 36
B 【解析】设C(4,b),则k=4b, ∵△OAC与△OBC的面积相等, ∴×6×b=×9×4,解得b=6, ∴k=4×6=24, 故选:B.查看答案和解析>>
科目:初中数学 来源:2017年吉林省长春市中考数学模拟试卷(7) 题型:单选题
比﹣1小2的数是( )
A. ﹣3 B. ﹣2 C. ﹣1 D. 3
A 【解析】比?1小2的数是就是?1与2的差,即?1?2=?3. 故选:A.查看答案和解析>>
科目:初中数学 来源:山东省2018届九年级12月月考数学试卷 题型:单选题
如图,AB为⊙O的直径,点C在⊙O上,若∠C=16°,则∠BOC的度数是( )
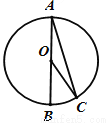
A. 74° B. 48° C. 32° D. 16°
C 【解析】∵OA=OC, ∴∠A=∠C=16°, ∴∠BOC=∠A+∠C=32°. 故选C。查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2016届九年级下学期二模数学试卷 题型:填空题
已知直角坐标内,半径为2的圆心坐标为(3,-4),当该圆向上平移m个单位长度时,若要此圆与x轴没有交点,则m的取值范围是 _______________.
m<2或m>6 【解析】圆心向上平移m个单位长度后坐标为(3,m-4), ∵圆与x轴没有交点, ∴所以圆心到x轴的距离>2, 即m-4>2或m-4<-2, ∴m>6或m<2. 故答案为m>6或m<2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com