练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，AB为⊙O的直径，点C在⊙O上，若∠C=16°,则∠BOC的度数是（ ）

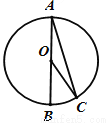
    A. 74° B. 48° C. 32° D. 16°

    C 【解析】∵OA=OC， ∴∠A=∠C=16°， ∴∠BOC=∠A+∠C=32°． 故选C。
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年吉林省中考数学一诊试卷 题型：单选题

    下列各式计算正确的是（ ）

    A. a+2a2=3a3 B. （a+b）2=a2+ab+b2

    C. 2（a﹣b）=2a﹣2b D. （2ab）2÷（ab）=2ab（ab≠0）

    C 【解析】A．不是同类项，不能合并，故A错误； B． ，故B错误； C．正确； D． = = ，故D错误． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷（7） 题型：填空题

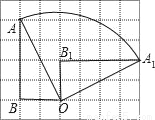
    如图，在小正方形的边长都为1的方格纸中，△ABO的顶点都在小正方形的顶点上，将△ABO绕点O顺时针方向旋转90°得到△A1B1O，则点A运动的路径长为_____．

    【解析】在Rt△ABO中,OA===； 根据题意,知OA=OA1. 又∵∠AOA1=90°， ∴点A旋转至A1点所经过的轨迹长度==π. 故答案是： π.

    查看答案和解析>>

    科目：初中数学 来源：山东省2018届九年级12月月考数学试卷 题型：解答题

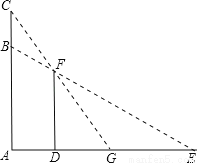
    如图，一只猫头鹰蹲在一棵树AC的B（点B在AC上）处，发现一只老鼠躲进短墙DF的另一侧，猫头鹰的视线被短墙遮住，为了寻找这只老鼠，它又飞至树顶C处，已知短墙高DF=4米，短墙底部D与树的底部A的距离为2.7米，猫头鹰从C点观测F点的俯角为53°，老鼠躲藏处M（点M在DE上）距D点3米．

    （参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）

    （1）猫头鹰飞至C处后，能否看到这只老鼠？为什么？

    （2）要捕捉到这只老鼠，猫头鹰至少要飞多少米（精确到0.1米）？

    （1）能看到（2）要捕捉到这只老鼠，猫头鹰至少要飞9.5米 【解析】试题分析：（1）根据猫头鹰从C点观测F点的俯角为53°，可知∠DFG=90°﹣53°=37°，在△DFG中，已知DF的长度，求出DG的长度，若DG＞3，则看不见老鼠，若DG＜3，则可以看见老鼠。 （2）根据（1）求出的DG长度，求出AG的长度，然后在Rt△CAG中，根据=sin∠C=sin37°，即可求出CG的长度。 ...

    查看答案和解析>>

    科目：初中数学 来源：山东省2018届九年级12月月考数学试卷 题型：填空题

    若x1=﹣1是关于x的方程x2+mx﹣5=0的一个根，则方程的另一个根x2=__．

    5 【解析】试题分析：首先将x=－1代入方程求出m的值，然后再去解关于x的一元二次方程．

    查看答案和解析>>

    科目：初中数学 来源：山东省2018届九年级12月月考数学试卷 题型：单选题

    方程x2－4＝0的解是（ ）

    A. x＝2 B. x＝－2 C. x＝±2 D. x＝±4

    C 【解析】试题分析：方程变形为x2=4，再把方程两边直接开方得到x=±2． 【解析】 x2=4， ∴x=±2． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：湖北省武汉市汉阳区2018届九年级（上）期中数学试卷（解析版） 题型：解答题

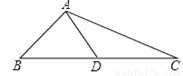
    如图，在△ABC中，AB=5，AC=13，边BC上的中线AD=6．

    （1）以点D为对称中心，作出△ABD的中心对称图形；

    （2）求点A到BC的距离．

    解析】 （1）答案见解析；（2）． 【解析】试题分析：(1)旋转180°得到的图形和原图形中心对称.(2) 作AM⊥BC于M,利用全等，三角形AEC,ABC等面积, AM•BD= •AB•AD，求AM的长度. 试题解析： 【解析】 （1）如图，△DCE即为所求. （2）作AM⊥BC于M，如图，AE=AD+DE=6+6=12， ∵△ABD与△ECD关于点D中心对...

    查看答案和解析>>

    科目：初中数学 来源：湖北省武汉市汉阳区2018届九年级（上）期中数学试卷（解析版） 题型：单选题

    用配方法解方程x2+10x+9=0，下列变形正确的是（　　）

    A. （x+5）2=16 B. （x+10）2=91

    C. （x﹣5）2=34 D. （x+10）2=109

    A 【解析】x2+10x+9=0， （x+5）2+25=-9+25， （x+5）2=16.故选A.

    查看答案和解析>>

    科目：初中数学 来源：2017年海南省海口市中考数学模拟试卷 题型：单选题

    如图，直线a，b被直线c所截，a∥b，∠1=∠2，若∠4=70°，则∠3等于（ ）

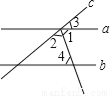
    A. 40° B. 50° C. 70° D. 80°

    A 【解析】试题分析：：∵∠1=∠2，∠3=40°，∴∠1=×（180°-∠3）=×（180°-40°）=70°， ∵a∥b，∴∠4=∠1=70°．故选：C．

    查看答案和解析>>

    同步练习册答案