
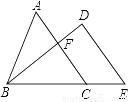
如图,△ABC与△DBE中,AC∥DE,点B、C、E在同一直线上,AC,BD相交于点F,若∠BDE=85°,∠BAC=55°,∠ABD:∠DBE=3:4,求∠DBE的度数.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2017年浙江省台州市中考数学二模试卷 题型:填空题
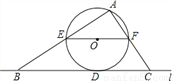
如图,直线l与⊙相切于点D,过圆心O作EF∥l交⊙O于E、F两点,点A是⊙O上一点,连接AE,AF,并分别延长交直线于B、C两点;若⊙的半径R=5,BD=12,则∠ACB的正切值为 ______ .
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题七年级人教版数学试卷(B卷) 题型:解答题
一架飞机由甲地飞往乙地,顺飞飞行要2.8小时,逆风飞行要3小时,风速为24km/h,求:
(1)无风时这架飞机的航速?
(2)两地的距离?
(1)飞机无风时的航速为每小时696km;(2)两城之间的距离为2016km. 【解析】试题分析:应先设出飞机在无风时的速度为,从而可知在顺风时的速度为飞机在无风中的速度加上风速,飞机在逆风中的速度等于飞机在无风中的速度减去风速,又已知了顺风飞行和逆风飞行所用的时间,再根据路程相等,列出等式,求解即可. 试题解析:设无风时飞机的航速为,根据题意得方程: 解方程得: 则两城之...查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题七年级人教版数学试卷(B卷) 题型:单选题
甲队有工人272人,乙队有工人196人,如果要求乙队的人数是甲队人数的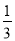 ,应从乙队调多少人去甲队.如果设应从乙队调x人到甲队,列出的方程正确的是( )
,应从乙队调多少人去甲队.如果设应从乙队调x人到甲队,列出的方程正确的是( )
A. 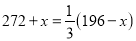 B.
B. 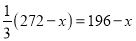
C. 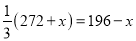 D.
D. 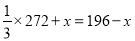
查看答案和解析>>
科目:初中数学 来源:重庆市2017年中考数学二模试卷 题型:解答题
如图,已知等腰Rt△ABC,∠ACB=90°,CA=CB,以BC为边向外作等边△CBA,连接AD,过点C作∠ACB的角平分线与AD交于点E,连接BE.
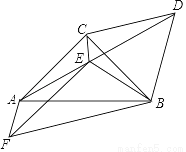
(1)若AE=2,求CE的长度;
(2)以AB为边向下作△AFB,∠AFB=60°,连接FE,求证:FA+FB= 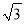 FE.
FE.
查看答案和解析>>
科目:初中数学 来源:重庆市2017年中考数学二模试卷 题型:填空题
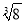 ﹣(2﹣
﹣(2﹣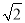 )0+(﹣
)0+(﹣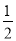 )﹣1=________.
)﹣1=________.
查看答案和解析>>
科目:初中数学 来源:重庆市2017年中考数学二模试卷 题型:单选题
△ADE∽△ABC,且相似比为1:3,若△ADE的面积为5,则△ABC的面积为( )
A. 10 B. 15 C. 30 D. 45
D 【解析】【解析】 ∵△ADE∽△ABC,且相似比为1:3,∴面积比为:1:9. ∵△DEF的面积为5,∴△ABC的面积为:5×9=45.故选D.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题七年级浙教版数学试卷(A卷) 题型:填空题
方程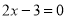 的解是_________________.
的解是_________________.
查看答案和解析>>
科目:初中数学 来源:2017年安徽省合肥市高新区梦园学校中考数学模拟试卷 题型:解答题
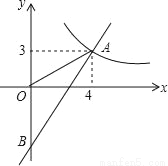
如图,一次函数y=kx+b的图象分别与反比例函数y=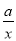 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)求函数y=kx+b和y=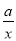 的表达式;
的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com