练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知∠α，∠β和线段c，求作△ABC，使∠A= ∠α，∠B=∠β，AB=c.（不写作法，保留痕迹）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2018年浙江省温州市六校联考数学试卷 题型：填空题

    如图，点A（1，b）在反比例函数的图象上，点B的坐标为（3，3），连结AB.以点B为旋转中心，将线段AB顺时针旋转900，得到线段BA′,延长BA′至C，使得BC=3BA′.以线段AB所在直线为对称轴，将C对称得到C′，若C′也在该反比例函数图象上，则_____.

    查看答案和解析>>

    科目：初中数学 来源：湖北省襄阳市2018年中考数学试卷 题型：解答题

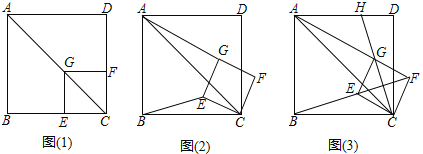
    如图（1），已知点G在正方形ABCD的对角线AC上，GE⊥BC，垂足为点E，GF⊥CD，垂足为点F．

    （1）证明与推断：

    ①求证：四边形CEGF是正方形；

    ②推断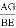：的值为　 　：

    （2）探究与证明：

    将正方形CEGF绕点C顺时针方向旋转α角（0°＜α＜45°），如图（2）所示，试探究线段AG与BE之间的数量关系，并说明理由：

    （3）拓展与运用：

    正方形CEGF在旋转过程中，当B，E，F三点在一条直线上时，如图（3）所示，延长CG交AD于点H．若AG=6，GH=2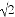，则BC=　 　．

    查看答案和解析>>

    科目：初中数学 来源：湖北省襄阳市2018年中考数学试卷 题型：单选题

    如图，在△ABC中，分别以点A和点C为圆心，大于AC长为半径画弧，两弧相交于点M，N，作直线MN分别交BC，AC于点D，E．若AE=3cm，△ABD的周长为13cm，则△ABC的周长为（　　）

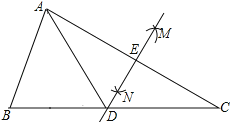
    A. 16cm B. 19cm C. 22cm D. 25cm

    查看答案和解析>>

    科目：初中数学 来源：广东省2017-2018学年七年级6月月考数学试卷 题型：解答题

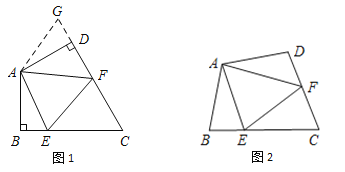
    （1）如图1，在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°，EF分别是 BC，CD上的点，且∠EAF＝60°，探究图中线段BE，EF，FD之间的数量关系．

    小王同学探究此问题的方法是延长FD到点G，使DG＝BE，连结AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是 ；

    探索延伸：

    （2）如图2，若在四边形ABCD中，AB＝AD，∠B＋∠D＝180°，E，F分别是BC，CD上的点，且∠EAF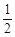＝∠BAD，上述结论是否仍然成立，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源：广东省2017-2018学年七年级6月月考数学试卷 题型：单选题

    如图，在△ABC中，∠C=90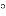，AC=BC，AD平分∠CAB交BC于点D,DE⊥AB于点E，且AB=6cm，则△DEB的周长是( )

    A. 6cm B. 4cm C. 10cm D. 以上都不对

    查看答案和解析>>

    科目：初中数学 来源：广东省2017-2018学年七年级6月月考数学试卷 题型：单选题

    如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是（ ）

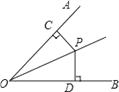
    A. PC=PD B. ∠CPD=∠DOP C. ∠CPO=∠DPO D. OC=OD

    查看答案和解析>>

    科目：初中数学 来源：安徽省桐城市2017-2018学年第二学期八年级期末学情检测 题型：填空题

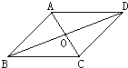
    如图已知四边形ABCD中，AB=CD，AB//CD要使四边形ABCD是菱形，应添加的条件是_____________________________（只填写一个条件，不使用图形以外的字母）.

    查看答案和解析>>

    科目：初中数学 来源：台湾省2018年中考数学试卷 题型：单选题

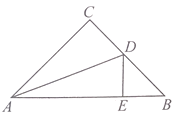
    如图，△ABC、△FGH中，D、E两点分别在AB、AC上，F点在DE上，G、H两点在BC上，且DE∥BC，FG∥AB，FH∥AC，若BG：GH：HC=4：6：5，则△ADE与△FGH的面积比为何？（　　）

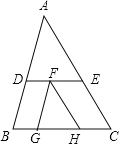
    A. 2：1 B. 3：2 C. 5：2 D. 9：4

    查看答案和解析>>

    同步练习册答案