练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    （1）如图1，在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°，EF分别是 BC，CD上的点，且∠EAF＝60°，探究图中线段BE，EF，FD之间的数量关系．

    小王同学探究此问题的方法是延长FD到点G，使DG＝BE，连结AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是 ；

    探索延伸：

    （2）如图2，若在四边形ABCD中，AB＝AD，∠B＋∠D＝180°，E，F分别是BC，CD上的点，且∠EAF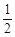＝∠BAD，上述结论是否仍然成立，并说明理由．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2018年浙江省温州市六校联考数学试卷 题型：解答题

    如图，在方格纸中，点A，D都在格点上，作三角形ABC，使其满足下列条件.（点B，C不与点D重合）

    （1）在图甲中，作格点等腰△ABC，使AD为△ABC的高线.

    （2）在图乙中，作格点钝角△ABC，使AD为△ABC的角平分线

    查看答案和解析>>

    科目：初中数学 来源：湖南省邵阳市2018年中考冲刺数学模拟试卷一 题型：单选题

    一组数据7，9，6，8，10，12中，下面说法正确的是( )

    A. 中位数等于平均数 B. 中位数大于平均数

    C. 中位数小于平均数 D. 中位数是8

    查看答案和解析>>

    科目：初中数学 来源：湖北省襄阳市2018年中考数学试卷 题型：填空题

    计算的结果是_____．

    查看答案和解析>>

    科目：初中数学 来源：湖北省襄阳市2018年中考数学试卷 题型：单选题

    不等式组的解集为（　　）

    A. x＞ B. x＞1 C. ＜x＜1 D. 空集

    查看答案和解析>>

    科目：初中数学 来源：广东省2017-2018学年七年级6月月考数学试卷 题型：解答题

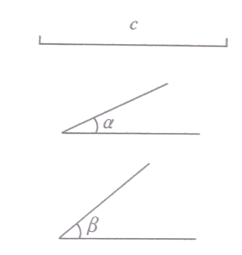
    已知∠α，∠β和线段c，求作△ABC，使∠A= ∠α，∠B=∠β，AB=c.（不写作法，保留痕迹）

    查看答案和解析>>

    科目：初中数学 来源：广东省2017-2018学年七年级6月月考数学试卷 题型：单选题

    如图，AB⊥BC，BE⊥AC，∠1=∠2，AD=AB，则（ ）

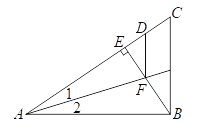
    A. ∠1=∠EFD B. BE=EC C. BF=DF=CD D. FD∥BC

    查看答案和解析>>

    科目：初中数学 来源：安徽省桐城市2017-2018学年第二学期八年级期末学情检测 题型：解答题

    解方程：2x2﹣4x+1=0.(用配方法)

    查看答案和解析>>

    科目：初中数学 来源：重庆市2017-2018学年八年级下学期期末第二次模拟考试数学试卷 题型：单选题

    下列各式一定是二次根式的是( )

    A. B. C. D.

    查看答案和解析>>

    同步练习册答案