
先化简,再求值:(a2b+ab)÷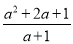 ,其中a=
,其中a=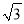 +1,b=
+1,b=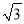 -1.
-1.
科目:初中数学 来源:山东省临沂市经济开发区2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
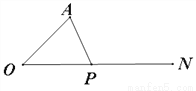
如图,已知点P是射线ON上一动点(即P可在射线ON上运动),∠AON=45°,当∠A=________时,△AOP为等腰三角形.
三、解答题(共60分)
45°或67.5°或90° 【解析】试题解析: ①是顶角时, ②是顶角时, ③是顶角时, 综上所述, 所有可能的度数为:45°或67.5°或90°. 故答案为:45°或67.5°或90°.查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学第20章数据的分析单元检测卷 题型:填空题
超市决定招聘广告策划人员一名,某应聘者三项素质测试的成绩如表:
测试项目 | 创新能力 | 综合知识 | 语言表达 |
测试成绩(分数) | 70 | 80 | 92 |
将创新能力、综合知识和语言表达三项测试成绩按5:3:2的比例计入总成绩,则该应聘者的总成绩是 分.
77.4. 【解析】试题分析:根据该应聘者的总成绩=创新能力×所占的比值+综合知识×所占的比值+语言表达×所占的比值可得该应聘者的总成绩是:70×+80×+92×=77.4分.查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学第20章数据的分析单元检测卷 题型:单选题
某校七年级有13名同学参加百米竞赛,预赛成绩各不相同,要取前6名参加决赛,小梅已经知道了自己的成绩,她想知道自己能否进入决赛,还需要知道这13名同学成绩的( )
A.中位数 B.众数 C.平均数 D.极差
A 【解析】 试题分析:由于有13名同学参加百米竞赛,要取前6名参加决赛,故应考虑中位数的大小. 【解析】 共有13名学生参加竞赛,取前6名,所以小梅需要知道自己的成绩是否进入前六. 我们把所有同学的成绩按大小顺序排列,第7名学生的成绩是这组数据的中位数, 所以小梅知道这组数据的中位数,才能知道自己是否进入决赛. 故选:A.查看答案和解析>>
科目:初中数学 来源:2018届中考数学一轮复习单元检测:第4讲 二次根式 题型:单选题
下列运算正确的是( )
A. 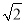 +
+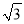 =
=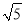 B. 2
B. 2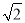 ×3
×3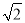 =6
=6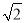
C. 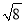 ÷
÷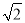 =2 D. 3
=2 D. 3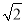 -
-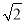 =3
=3
查看答案和解析>>
科目:初中数学 来源:2018届中考数学一轮复习单元检测:第4讲 二次根式 题型:单选题
关于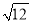 的叙述,错误的是( )
的叙述,错误的是( )
A. 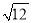 是有理数
是有理数
B. 面积为12的正方形的边长是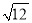
C. 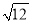 =2
=2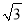
D. 在数轴上可以找到表示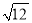 的点
的点
查看答案和解析>>
科目:初中数学 来源:人教版初中数学七年级下册第六章 《平方根》同步练习 题型:填空题
计算: 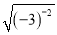 +(|﹣3|)0=_____.
+(|﹣3|)0=_____.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学人教版上册:第1、2章单元测试卷 题型:解答题
先化简,再求值:
(1)2m2-4m+1-2(m2+2m-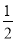 ),其中m=-1;
),其中m=-1;
(2)5xy2-[2x2y-(2x2y-3xy2)],其中(x-2)2+|y+1|=0.
(1) -8m+2,10; (2) 2xy2,4. 【解析】试题分析:(1)原式去括号合并得到最简结果,把m的值代入计算即可求出值; (2)原式去括号合并得到最简结果,利用非负数的性质求出x与y的值,代入原式计算即可得到结果. 试题解析:(1)原式=2m2-4m+1-2m2-4m+1=-8m+2. 当m=-1时,原式=8+2=10. (2)原式=5xy2-2x2y+2...查看答案和解析>>
科目:初中数学 来源:山东省临沂市经济开发区2018届九年级上学期期末考试数学试卷 题型:解答题
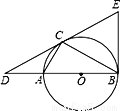
已知△ABC内接于以AB为直径的⊙O,过点C作⊙O的切线交BA的延长线于点D,且DA∶AB=1∶2.
(1)求∠CDB的度数;
(2)在切线DC上截取CE=CD,连接EB,判断直线EB与⊙O的位置关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com