
 已知△ABC,延长BC到D,使CD=BC.取AB的中点F,连结FD交AC于点E.
已知△ABC,延长BC到D,使CD=BC.取AB的中点F,连结FD交AC于点E. 的值;
的值; 解:(1)如图,连接FC、AD.
解:(1)如图,连接FC、AD.
 AD,
AD, =
= =2,
=2, =
= ;
; AB=9.
AB=9. =2,则
=2,则 =2,故AE=18,
=2,故AE=18,
 AD;然后由“平行法”证得△EFC∽△EDA,则该相似三角形的对应边成比例:
AD;然后由“平行法”证得△EFC∽△EDA,则该相似三角形的对应边成比例: =
= =2,所以由比例的性质可以求得
=2,所以由比例的性质可以求得 的值;
的值; AB=FB=EC=9代入,即可求得AC的长度.
AB=FB=EC=9代入,即可求得AC的长度.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
 如图,已知△ABC,延长AC.
如图,已知△ABC,延长AC.查看答案和解析>>
科目:初中数学 来源:第27章《相似》中考题集(18):27.2 相似三角形(解析版) 题型:解答题
 的值;
的值;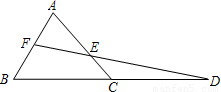
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com