
已知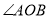 与
与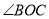 互为补角,
互为补角, 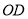 是
是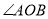 的角平分线,射线
的角平分线,射线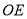 在
在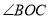 内,且
内,且 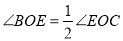 ,
, 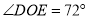 ,求
,求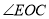 的度数.
的度数.
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源:湖南省2018届九年级数学上期末复习检测数学试卷 题型:解答题
关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根x1 , x2 ,求实数k的取值范围.
k> . 【解析】试题分析:根据方程有两个不相等的实数根可得△=(2k+1)2-4(k2+1)>0,解不等式即可求出k的取值范围. 试题解析:∵原方程有两个不相等的实数根, ∴△=(2k+1)2-4(k2+1)=4k2+4k+1-4k2-4=4k-3>0, 解得:k> .查看答案和解析>>
科目:初中数学 来源:湖北省十堰市2017-2018学年七年级(上)期中数学试卷 题型:单选题
下列各组中,不是同类项的是( )
A. ﹣x2y与2yx2 B. 2ab与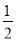 ba C. ﹣m2n与
ba C. ﹣m2n与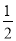 mn2 D. 23和32
mn2 D. 23和32
查看答案和解析>>
科目:初中数学 来源:安徽省巢湖市2016~17学年度第一学期 期末教学质量检测 八年级数学试卷 题型:填空题
如图,在⊿ABC和⊿FED中,AD=FC,AB=FE,当添加条件______________时,就可以得到⊿ABC≌⊿FED.(只需填写一个你认为正确的条件)
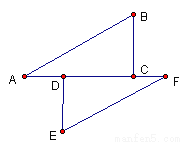
查看答案和解析>>
科目:初中数学 来源:安徽省巢湖市2016~17学年度第一学期 期末教学质量检测 八年级数学试卷 题型:单选题
如图,在△ABC中,AC=4 cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7 cm,则BC的长为( )
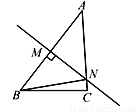
A. 1 cm B. 2 cm C. 3 cm D. 4 cm
C 【解析】试题分析:根据中垂线的性质可得:BN=AN,则△BCN的周长=BN+NC+BC=AN+NC+BC=AC+BC=7cm,根据AC=4cm可得:BC=7-4=3cm.查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年七年级数学上期末复习检测数学试卷 题型:解答题
若(2a+4)2+|4b﹣4|=0,求a+b的值?
﹣1 【解析】试题分析:根据非负数的性质列出方程求出a、b的值,代入所求代数式计算即可. 试题解析:由题意得,2a+4=0,4b﹣4=0, 解得,a=﹣2,b=1, 故a+b=﹣2+1=﹣1.查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年七年级数学上期末复习检测数学试卷 题型:填空题
若a,b互为倒数,c,d互为相反数,则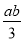 ﹣c﹣d=________.
﹣c﹣d=________.
查看答案和解析>>
科目:初中数学 来源:黑龙江省2017-2018学年七年级数学上学期期末试卷 题型:解答题
如图,M是线段AC中点,点B在线段AC上,且AB=4cm,BC=2AB,求线段MC和线段BM的长.
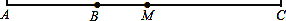
查看答案和解析>>
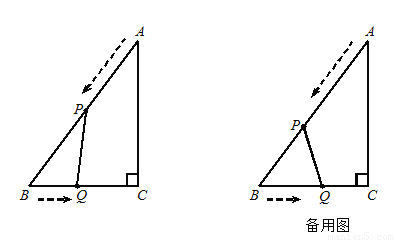
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市九年级数学科期末检测题 题型:解答题
如图12,在△ABC中,∠C=90°,AB=10cm,BC=6cm. 点P从点A出发,沿AB边以2 cm/s的速度向点B匀速移动;点Q从点B出发,沿BC边以1 cm/s的速度向点C匀速移动. 当一个运动点到达终点时,另一个运动点也随之停止运动,设运动的时间为t(s).
(1)当PQ∥AC时,求t的值;
(2)当t为何值时,QB=QP;
(3)当t为何值时,△PBQ的面积等于4.8cm 2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com