练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    一个多边形的内角和是外角和的5倍,则这个多边形是 (　　)

    A. 八边形 B. 十边形

    C. 十二边形 D. 十四边形

    C 【解析】多边形的外角和是360°，设这个多边形的边数为x，则 180°（x-2）=5×360，解得x=12. 故选C.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教版九年级上册数学 24.2.2直线和圆的位置关系（2）练习 题型：单选题

    下列四边形中一定有内切圆的是（）

    A. 直角梯形 B. 等腰梯形 C. 矩形 D. 菱形

    D 【解析】根据内切圆的定义即角平分线的交点到各边的距离相等,可知菱形一定有内切圆,故选D.

    查看答案和解析>>

    科目：初中数学 来源：同步练习3：1.1菱形的性质与判定 题型：单选题

    下列命题中，真命题是（ ）

    A. 对角线互相垂直且相等的四边形是菱形

    B. 对角线互相垂直的平行四边形是菱形

    C. 对角线互相平分且相等的四边形是菱形

    D. 对角线相等的四边形是菱形

    B 【解析】试题分析：A．不能判断是否为菱形，故A错误； B．对角线互相垂直的平行四边形是菱形，正确； C．对角线相等且互相平分的四边形是矩形，故C错误； D．不能判断是否为菱形；故D错误； 故选B．

    查看答案和解析>>

    科目：初中数学 来源：北师大版（贵州）八年级数学下册：期末综合检测 题型：填空题

    对于任意实数m、n，定义一种运算m※n=mn﹣m﹣n+3，等式的右边是通常的加减和乘法运算，例如：3※5=3×5﹣3﹣5+3=10．请根据上述定义解决问题：若a＜2※x＜7，且解集中有两个整数解，则a的取值范围是_____．

    4≤a＜5 【解析】试题分析：根据题意得：2※x=2x﹣2﹣x+3=x+1，∵a＜x+1＜7，即a﹣1＜x＜6解集中有两个整数解，∴a的范围为，故答案为： ．

    查看答案和解析>>

    科目：初中数学 来源：北师大版（贵州）八年级数学下册：期末综合检测 题型：单选题

    如图所示,四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定这个四边形是平行四边形的是 (　　)

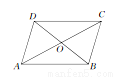
    A. AB∥DC,AD∥BC

    B. AB=DC,AD=BC

    C. AO=CO,BO=DO

    D. AB∥DC,AD=BC

    D 【解析】试题分析：A、根据两组对边分别平行的四边形为平行四边形；B、根据两组对边分别相等的四边形为平行四边形；C、根据对角线互相平分的四边形是平行四边形；D、不能判定.

    查看答案和解析>>

    科目：初中数学 来源：浙江杭州西湖区第十三中学2017-2018学年八年级上学期中考试数学试卷（含解析） 题型：解答题

    如图，在中，，，是的平分钱，垂足是，和的延长线交于点．

    （）请找出与相等的所有的角，并证明其中一个．

    （）求证：．

    （），理由见解析；（2）证明见解析. 【解析】试题分析：（1）与∠F相等的所有角为∠ADB、∠EDC、∠BCF，选择证明∠F=∠BCF，由已知条件不难证明△FBE≌△CBE，即可证明∠F=∠BCF；（2）先计算出∠ABC和∠ACB的度数，继而求出∠ABD的度数，再由等腰三角形中，已知顶角∠ABC的度数，求出底角∠FCB的度数，接着求出∠ACF的度数，得出∠ABD=∠FCA，再由AB=AC以及...

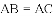
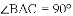
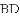
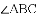
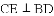
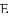
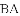
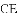
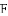
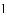
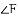
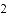
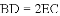
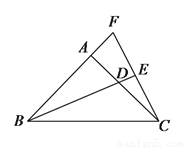
    查看答案和解析>>

    科目：初中数学 来源：浙江杭州西湖区第十三中学2017-2018学年八年级上学期中考试数学试卷（含解析） 题型：填空题

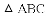
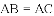
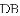
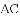
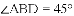
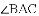
    在中，，是边上的高线，且．则等于__________．

    或 【解析】 如图，∵BD⊥AC，∠ABD=45°， ∴∠BAC=45°； 如图，∠BAC=∠D+∠ABD=135°. 故答案为45°或135°.

    查看答案和解析>>

    科目：初中数学 来源：2017年内蒙古呼和浩特市中考数学试卷六 题型：解答题

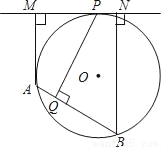
    如图，MN切⊙O于P，AB是⊙O的弦，AM⊥MN于M，BN⊥MN于N，PQ⊥AB于Q．

    求证：PQ2=AM•BN．

    答案见解析 【解析】试题分析：连接根据垂直的定义得到，根据相似三角形的性质得到 同理可得： 等量代换得到 于是得到结论． 试题解析：证明：连接 ∵于，于． 同理可得：

    查看答案和解析>>

    科目：初中数学 来源：2016--2017学年度江西省赣县区第二学期期中考试七年级数学试卷 题型：单选题

    如图,直线AB∥CD,∠C=44°,∠E=90°,则∠1等于(　　)

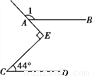
    A. 132° B. 134° C. 136° D. 138°

    B 【解析】过E作EF∥AB，求出AB∥CD∥EF，根据平行线的性质得出∠C=∠FEC，∠BAE=∠FEA，求出∠BAE，即可求出答案． 【解析】 过E作EF∥AB， ∵AB∥CD， ∴AB∥CD∥EF， ∴∠C=∠FEC，∠BAE=∠FEA， ∵∠C=44°，∠AEC为直角， ∴∠FEC=44°，∠BAE=∠AEF=90°﹣44°=46°， ...

    查看答案和解析>>

    同步练习册答案