
��������ʵ��m��n������һ������m��n=mn��m��n+3����ʽ���ұ���ͨ���ļӼ��ͳ˷����㣬���磺3��5=3��5��3��5+3=10��������������������⣺��a��2��x��7���ҽ⼯�������������⣬��a��ȡֵ��Χ��_____��
4��a��5 �������������������������ã�2��x=2x��2��x+3=x+1����a��x+1��7����a��1��x��6�⼯�������������⣬��a�ķ�ΧΪ���ʴ�Ϊ�� �� ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017��ʦ�����ѧ���꼶�ϲ� ��4�� һ�κ��� ��Ԫ����� ���ͣ���ѡ��
���ڵ�һ�κ���y��kx��k2��1��ͼ�������(����)
A. 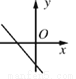 B.
B. 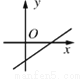 C.
C. 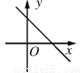 D.
D. 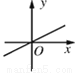
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ͬ����ϰ3��1.1���ε��������ж� ���ͣ������
�����ε������Խ��ߵı�Ϊ3:4�����ܳ�Ϊ20cm��������һ��Աߵľ������________cm,�����������_________cm2.
24 ����������ͼ����֪�����ܳ�Ϊ20cm����AB=5cm����BO=4x����AO=3x���������ζԽ����ഹֱƽ�ֺ��ɶ����ɵ� �����x=1����AO=3cm��BO=4cm���������ε����ΪS=��6cm��8cm=24cm2��AE= cm.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�ϲ���ѧ 25.2���оٷ�����ʲ��� ���ͣ������
��1��2����3�������У������ȡ��������ˣ����������ĸ����� ��
�� ��������������������ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ���������ȡ��������ˣ���������������������ø��ʹ�ʽ��⼴����ô𰸣� �������� ����״ͼ�ã� �߹���6�ֵȿ��ܵĽ���������ȡ��������ˣ�������������2������� �������ȡ��������ˣ����������ĸ����ǣ�=�� �ʴ�Ϊ�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ��棨���ݣ����꼶��ѧ�²��ĩ�ۺϼ�� ���ͣ������
��2015���ݣ�ѧУΪ�˽������������ҵ�����ƻ�����һ��ƽ����Ժ�һ��ѧϰ������Ͷ�꣬����1̨ƽ����Աȹ���3̨ѧϰ����600Ԫ������2̨ƽ����Ժ�3̨ѧϰ������8400Ԫ��
��1������1̨ƽ����Ժ�1̨ѧϰ���������Ԫ��
��2��ѧУ����ʵ���������������ƽ����Ժ�ѧϰ����100̨��Ҫ������ܷ��ò�����168000Ԫ���ҹ���ѧϰ����̨������������ƽ�����̨����1.7�����������ļ��ֹ��������ַ�����ʡǮ��
��1������1̨ƽ�������3000Ԫ������1̨ѧϰ����800Ԫ����2������1������ƽ�����38̨��ѧϰ��62̨������2������ƽ�����39̨��ѧϰ��61̨������3������ƽ�����40̨��ѧϰ��60̨������1��ʡǮ�� �������������������1���蹺��1̨ƽ�������xԪ������1̨ѧϰ����yԪ���������г������飬���������Ľ�õ�x��y��ֵ�����ɵõ������ ��2���蹺��ƽ�����x̨��ѧϰ����100��...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ��棨���ݣ����꼶��ѧ�²��ĩ�ۺϼ�� ���ͣ���ѡ��
ƽ���ı���ABCD�У�E��F�ǶԽ���BD�ϵ����㣬 �������һ������ʹ��ABE�ա�CDF�������ӵ����������ǣ�������
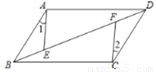
A. AE=CF B. BE=FD C. BF=DE D. ��1=��2
C �������������������Ϊ�ı���ABCD��ƽ���ı��Σ�����AB//CD,AB=CD�����ԡ�ABD=��CDB,����Ҫʹ��ABE�ա�CDF�� ��������������1=��2����������ASA֤����ABE�ա�CDF������D��ȷ��������������BE=FD����������SAS֤����ABE�ա�CDF������B��ȷ��������������BF=DE�����Եõ�BE=FD����������SAS֤����ABE�ա�CDF������C��ȷ����������...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ��棨���ݣ����꼶��ѧ�²��ĩ�ۺϼ�� ���ͣ���ѡ��
һ������ε��ڽǺ�����Ǻ͵�5��,������������ (����)
A. �˱��� B. ʮ����
C. ʮ������ D. ʮ�ı���
C ������������ε���Ǻ���360�㣬���������εı���Ϊx���� 180�㣨x-2��=5��360�����x=12. ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭������������ʮ����ѧ2017-2018ѧ����꼶��ѧ���п�����ѧ�Ծ����������� ���ͣ���ѡ��
��ͼ����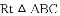
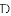
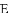
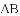
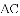
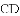
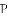
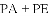
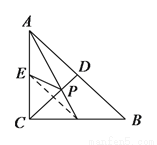
A. 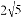 B.
B. 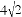 C.
C. 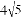 D.
D. 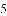
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016--2017ѧ��Ƚ���ʡ�������ڶ�ѧ�����п������꼶��ѧ�Ծ� ���ͣ������
��֪x��2��ƽ�����ǡ�2�� 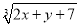 ��3����x2��y2��ƽ������
��3����x2��y2��ƽ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com