
科目:初中数学 来源:黑龙江省密山市2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
若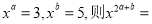 ( )
( )
A. 45 B. 30 C. 15 D. 11
A 【解析】∵ ∴= 故选A.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷(A卷) 题型:填空题
抛物线y=2x2﹣4x+1的对称轴为直线__.
x=1 【解析】【解析】 ∵y=2x2﹣4x+1=2(x﹣1)2﹣1,∴对称轴为直线x=1,故答案为:x=1.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷(A卷) 题型:单选题
下列图形中,既是轴对称图形又是中心对称图形的是( )
A.  B.
B. 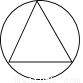 C.
C. 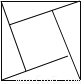 D.
D. 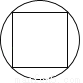
查看答案和解析>>
科目:初中数学 来源:河南省2017-2018学年八年级(上)第一次月考数学试卷 题型:解答题
如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,∠A=35°,∠D=42°,求∠ACD的度数.
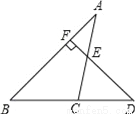
查看答案和解析>>
科目:初中数学 来源:河南省2017-2018学年八年级(上)第一次月考数学试卷 题型:单选题
如图所示,在下列条件中,不能作为判断△ABD≌△BAC的条件是( )
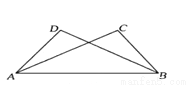
A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
C 【解析】试题分析:本题已知条件是两个三角形有一公共边,只要再加另外两边对应相等或有两角对应相等即可,如果所加条件是一边和一角对应相等,必须是这边和公共边的夹角对应相等,只有符合以上条件,才能根据三角形全等判定定理得出结论. 【解析】 A、符合AAS,能判断△ABD≌△BAC; B、符合ASA,能判断△ABD≌△BAC; C、符合SSA,不能判断△ABD≌△BAC; ...查看答案和解析>>
科目:初中数学 来源:广西南宁市2017年中考数学一模试卷 题型:解答题
如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.
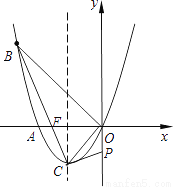
(1)求抛物线的函数解析式.
(2)设点D在抛物线上,点E在抛物线的对称轴上,若四边形AODE是平行四边形,求点D的坐标.
(3)联接BC交x轴于点F.y轴上是否存在点P,使得△POC与△BOF相似?若存在,求出点P的坐标;若不存在,请说明理由.
(1) y=x2+2x;(2) (1,3);(3) (0,﹣ )或(0,﹣4). 【解析】试题分析:(1)将点A、点B和原点代入解析式进行求解;(2)根据平行四边形的性质得出点D的坐标;(3)首先求出OB、OF、OC的长度,然后根据三角形相似的条件求出点P的坐标,分两种情况进行讨论. 试题解析:(1)设抛物线的解析式为y=ax2+bx+c(a≠0), 将点A(﹣2,0),B(﹣3...查看答案和解析>>
科目:初中数学 来源:广西南宁市2017年中考数学一模试卷 题型:单选题
小张抛掷两枚质地均匀的硬币,出现两枚硬币全部正面朝上的概率是( )
A. 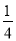 B.
B. 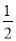 C.
C. 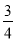 D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源:湖北省武汉市江夏区2017-2018学年八年级(上)期中数学试卷 题型:解答题
如图,在△ABD和△FEC中,点B、C、D、E在同一直线上,且AB=FE,BC=DE,∠B=∠E,求证:∠ADB=∠FCE.
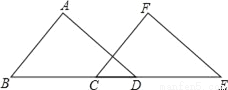
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com