
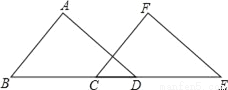
如图,在△ABD和△FEC中,点B、C、D、E在同一直线上,且AB=FE,BC=DE,∠B=∠E,求证:∠ADB=∠FCE.
科目:初中数学 来源:河南省2017-2018学年八年级(上)第一次月考数学试卷 题型:填空题
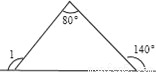
如图,∠1=_____.
查看答案和解析>>
科目:初中数学 来源:广西岑溪市2018届九年级上学期期中抽考数学试卷 题型:解答题
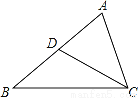
已知:如图,D是△ABC的边AB上一点,且∠B=∠ACD.求证:AC2=AD•AB.
查看答案和解析>>
科目:初中数学 来源:广西岑溪市2018届九年级上学期期中抽考数学试卷 题型:单选题
若点(x1,y1)、(x2,y2)和(x3,y3)分别在反比例函数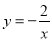 的图象上,且x1<x2<0<x3,则下列判断中正确的是( )
的图象上,且x1<x2<0<x3,则下列判断中正确的是( )
A. y1<y2<y3 B. y3<y1<y2 C. y2<y3<y1 D. y3<y2<y1
B 【解析】由题意,得点(x1,y1)、(x2,y2)在第二象限,(x3,y3)在第四象限, ∴y3最小, ∴x1<x2, ∴y1<y2, ∴y3<y1<y2. 故选B.查看答案和解析>>
科目:初中数学 来源:湖北省武汉市江夏区2017-2018学年八年级(上)期中数学试卷 题型:解答题
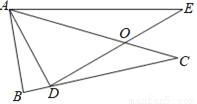
如图所示,已知△ABC中,D为BC上一点,E为△ABC外部一点,DE交AC于一点O,AC=AE,AD=AB,∠BAC=∠DAE.
(1)求证:△ABC≌△ADE;
(2)若∠BAD=20°,求∠CDE的度数.
查看答案和解析>>
科目:初中数学 来源:湖北省武汉市江夏区2017-2018学年八年级(上)期中数学试卷 题型:填空题
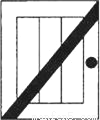
如图,为了使一扇旧木门不变形,木工师傅在木门的背后加钉了一根木条,这样做的道理是_____.
查看答案和解析>>
科目:初中数学 来源:湖北省武汉市江夏区2017-2018学年八年级(上)期中数学试卷 题型:单选题
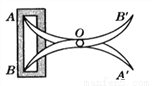
如图,将两根钢条AA′,BB′ 的中点O钉在一起,使AA′,BB′ 能绕点O自由转动,就做成一个测量工具,测A′B′ 的长即等于内槽宽AB,那么判定△OAB ≌△OA′B′的理由是( ).
A. 边角边 B. 角边角 C. 边边边 D. 斜边直角边
A 【解析】由题意得边角边可得全等.故选A.查看答案和解析>>
科目:初中数学 来源:2017年河北省中考数学三模试卷 题型:单选题
函数y=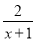 的图象可能是( )
的图象可能是( )
A. 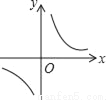 B.
B. 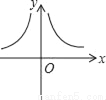 C.
C. 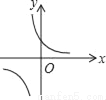 D.
D. 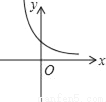
查看答案和解析>>
科目:初中数学 来源:2017年海南省中考数学模拟试卷 题型:解答题
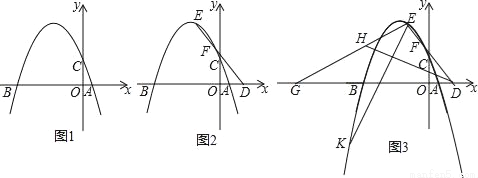
如图1,已知抛物线y=﹣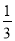 x2﹣
x2﹣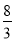 x+c与x轴相交于A、B两点(B点在A点的左侧),与y轴相交于C点,且AB=10.
x+c与x轴相交于A、B两点(B点在A点的左侧),与y轴相交于C点,且AB=10.
(1)求这条抛物线的解析式;
(2)如图2,D点在x轴上,且在A点的右侧,E点为抛物线上第二象限内的点,连接ED交抛物线于第二象限内的另外一点F,点E到y轴的距离与点F到y轴的距离之比为3:1,已知tan∠BDE=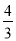 ,求点E的坐标;
,求点E的坐标;
(3)如图3,在(2)的条件下,点G由B出发,沿x轴负方向运动,连接EG,点H在线段EG上,连接DH,∠EDH=∠EGB,过点E作EK⊥DH,与抛物线相应点E,若EK=EG,求点K的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com