练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若分式方程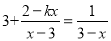无解,则k=__________

    3和1 【解析】试题解析：方程去分母得：3（x-3）+2-kx=-1， 整理得（3-k）x=6， 当整式方程无解时，3-k=0即k=3， 当分式方程无解时，x=3，此时3-k=2，k=1， 所以k=3或1时，原方程无解． 故答案为：3或1．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：山西省吕梁市孝义市2016-2017学年九年级（上）期末考试数学试卷 题型：填空题

    在扇形纸片AOB中，∠AOB=90°，OA=4，将扇形纸片AOB按如图所示折叠，使对折后点A与点O重合，折痕为DE，则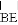的长度为__________．

    【解析】试题分析：连接OE， ∵将扇形纸片AOB按如图所示折叠，使对折后点A与点O重合，折痕为DE， ∴OD＝OA＝OE，∠EDO＝90°， ∴∠DEO＝30°， ∴∠DOE＝60°， ∵∠AOB＝90°， ∴∠EOB＝30°， ∴弧BE的长度＝＝． 故答案为：．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学北师大版上册：第4章 基本平面图形 单元测试卷 题型：解答题

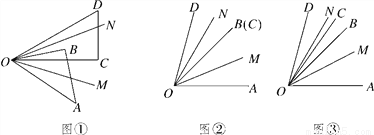
    如图①，将一副三角板的两个锐角顶点放到一块，∠AOB＝45°，∠COD＝30°，OM，ON分别是∠AOC，∠BOD的平分线．

    (1)当∠COD绕着点O逆时针旋转至射线OB与OC重合时(如图②)，则∠MON的大小为________；

    (2)如图③，在(1)的条件下，继续绕着点O逆时针旋转∠COD，当∠BOC＝10°时，求∠MON的大小，写出解答过程；

    (3)在∠COD绕点O逆时针旋转过程中，∠MON＝________°.

    （1）37.5°；（2）∠MON=37.5°；（3）37.5° 【解析】试题分析：(1)、根据角平分线的性质得出∠NOC=15°，∠MOC=22.5°，最后根据∠MON=∠NOC+∠MOC得出答案；(2)、首先根据∠BOC的度数求出∠AOC和∠BOD的度数，然后根据角平分线的性质求出∠BON和∠MOB的度数，最后根据∠MON=∠MOB+∠BON得出答案；(3)、根据题意得出∠AOC＝∠AOB...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学北师大版上册：第4章 基本平面图形 单元测试卷 题型：单选题

    如图，一条流水生产线上L1、L2、L3、L4、L5处各有一名工人在工作，现要在流水生产线上设置一个零件供应站P，使五人到供应站P的距离总和最小，这个供应站设置的位置是(　　)

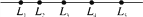
    A. L2处 B. L3处 C. L4处 D. 生产线上任何地方都一样

    B 【解析】试题分析：设在L3处为最佳，求出此时的总距离为L1L5+L2L4，假如设于任意的X处，求出总距离为L1L5+L2L4+L3X，和L1L5+L2L4比较即可． 【解析】 在5名工人的情况下，设在L3处为最佳，这时总距离为L1L5+L2L4， 理由是：如果不设于L3处，而设于X处，则总距离应为L1L5+L2L4+L3X＞L1L5+L2L4， 即在L3处5个工人到供...

    查看答案和解析>>

    科目：初中数学 来源：山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型：解答题

    如图,在平面直角坐标系中,A(-1，5)，B（-1，0），C（-4，3）.

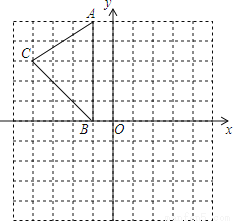
    （1）在图中作出△ABC关于y轴的对称图形△A1B1C1；
    （2）写出点A1、B1、C1的坐标；
    （3）在y轴上画出点P，使PA+PC最小；  
    （4）求六边形AA1C1B1BC的面积．.

    （1）作图见解析；（2）A1（1，5）、B1（1，0）、C1（4，3）；（3）见解析；（4）25. 【解析】试题分析：（1）根据题意画出△A1B1C1即可； （2）根据△A1B1C1在坐标系中的位置即可得出各点坐标； （3）连接A1C与y轴交于点P，则P点即为所求； （4）根据S六边形AA1C1B1BC=S△ABC+S△A1B1C1+S矩形AA1C1B1B即可得出结论． ...

    查看答案和解析>>

    科目：初中数学 来源：山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型：填空题

    一个凸多边形的内角和与外角和相等，它是______边形．

    四． 【解析】设这个正多边形的边数是n，则（n-2）•180°=360°，解得n=4．所以这个正多边形是四边形．

    查看答案和解析>>

    科目：初中数学 来源：山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型：单选题

    若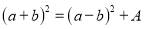,则A为(     )

    A. 2ab B. -2ab C. 4ab D. -4ab

    C 【解析】试题解析：∵（a+b）2=a2+2ab+b2，（a-b）2=a2-2ab+b2， ∴A=（a+b）2-（a-b）2=4ab． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型：填空题

    如图，在△ABC中，AB=4，BC=7，∠B=60°，将△ABC绕点A按顺时针旋转一定角度得到△ADE，当点B的对应点D恰好落在BC边上时，则CD的长为__________．

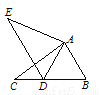
    3 【解析】试题解析: 由旋转的性质可得：AD=AB， ∴△ABD是等边三角形， ∴BD=AB， ∵AB=4，BC=7， ∴CD=BC?BD=7?4=3. 故答案为：3.

    查看答案和解析>>

    科目：初中数学 来源：广西合浦县2017年秋季学期教学质量监测七年级数学试卷 题型：解答题

    如图，阳光下，小亮的身高如图中线段AB所示，他在地面上的影子如图中线段BC所示，线段DE表示旗杆的高，线段FG表示一堵高墙．

    （1）请你在图中画出旗杆在同一时刻阳光照射下形成的影子，并用线段表示；

    （2）如果小亮的身高AB=1.6m，他的影子BC=2.4m，旗杆的高DE=15m，旗杆与高墙的距离EG=16m，请求出旗杆的影子落在墙上的长度．

    （1）作图见解析；（2）米. 【解析】试题分析：（1）连接AC，过D点作AC的平行线即可； （2）过M作MN⊥DE于N，利用相似三角形列出比例式求出旗杆的高度即可． 试题解析：（1）如图：线段MG和GE就表示旗杆在阳光下形成的影子． （2）过M作MN⊥DE于N， 设旗杆的影子落在墙上的长度为x，由题意得：△DMN∽△ACB， ∴ 又∵AB=1.6，BC=2...

    查看答案和解析>>

    同步练习册答案