
若二次函数y=-x2-4x+k的最大值是9,则k=______.
5 【解析】y=?(x?2)2+4+k, ∵二次函数y=?x2?4x+k的最大值是9, ∴4+k=9,解得:k=5, 故答案为:5.科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期中测试 题型:填空题
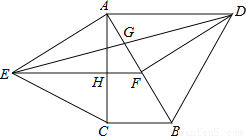
如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=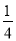 BD
BD
其中正确结论的为______(请将所有正确的序号都填上).
查看答案和解析>>
科目:初中数学 来源:青海省2017-2018学年七年级上学期12月月考数学试卷 题型:填空题
若2a﹣b=3,则多项式8a﹣4b+3的值是______.
15 【解析】试题解析: 故答案为:查看答案和解析>>
科目:初中数学 来源:甘肃省定西市安定区2017-2018学年九年级上学期期末考试数学试卷 题型:解答题
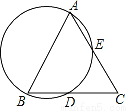
如图,点A、B、C、D、E在圆上,弦的延长线与弦的延长线相交于点,AB是圆的直径,D是BC的中点.求证:AB=AC.
查看答案和解析>>
科目:初中数学 来源:甘肃省定西市安定区2017-2018学年九年级上学期期末考试数学试卷 题型:填空题
二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴是直线x=1,有以下四个结论:
①abc>0;②b2-4ac>0;③b=-2a;④a+b+c>2.其中正确的是______(填写序号)
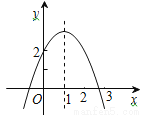
查看答案和解析>>
科目:初中数学 来源:甘肃省定西市安定区2017-2018学年九年级上学期期末考试数学试卷 题型:单选题
将抛物线y=x2-4x-4向左平移3个单位,再向上平移5个单位,得到抛物线的表达式为( )
A. y=(x+1)2-13 B. y=(x-5)2-3 C. y=(x-5)2-13 D. y=(x+1)2-3
A 【解析】先将一般式化为顶点式,根据左加右减,上加下减来平移 【解析】 将抛物线化为顶点式为: ,左平移3个单位,再向上平移5个单位 得到抛物线的表达式为 故选A. “点睛”本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考...查看答案和解析>>
科目:初中数学 来源:江苏省东台市第三教育联盟2017-2018学年度第一学期第三次阶段检测七年级数学试卷 题型:解答题
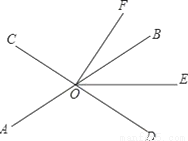
如图,直线AB、CD相交于点O,OE平分∠BOD.
(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.
①用含x的代数式表示∠EOF;
②求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源:江苏省东台市第三教育联盟2017-2018学年度第一学期第三次阶段检测七年级数学试卷 题型:填空题
若单项式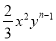 与单项式﹣5xmy3是同类项,则m﹣n的值为________.
与单项式﹣5xmy3是同类项,则m﹣n的值为________.
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 大题易丢分 题型:解答题
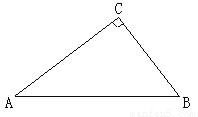
如图,在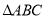 中,
中, 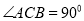 ,点
,点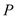 到
到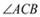 两边的距离相等,且
两边的距离相等,且 .
.
(1)先用尺规作出符合要求的点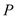 (保留作图痕迹,不需要写作法),然后判断△ABP的形状,并说明理由;
(保留作图痕迹,不需要写作法),然后判断△ABP的形状,并说明理由;
(2)设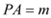 ,
,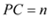 ,试用
,试用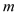 、
、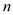 的代数式表示
的代数式表示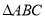 的周长和面积;
的周长和面积;
(3)设 与
与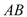 交于点
交于点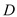 ,试探索当边
,试探索当边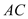 、
、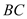 的长度变化时,
的长度变化时,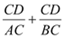 的值是否发生变化,若不变,试求出这个不变的值,若变化,试说明理由.
的值是否发生变化,若不变,试求出这个不变的值,若变化,试说明理由.
【答案】(1)作图见解析;ΔABP是等腰直角三角形. 理由见解析;(2)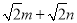 ;
; 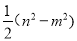 (3)
(3)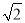 .
.
【解析】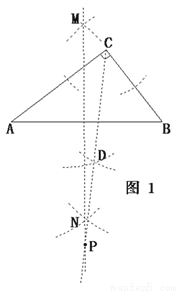 (1)依题意,点P既在
(1)依题意,点P既在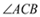 的平分线上,
的平分线上,
又在线段AB的垂直平分线上.
如图1,作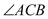 的平分线
的平分线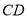 ,
,
作线段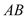 的垂直平分线
的垂直平分线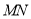 ,
, 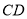 与
与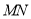 的
的
交点即为所求的P点。┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄3分
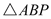 是等腰直角三角形.
是等腰直角三角形.
理由:过点P分别作 、
、 ,垂足为E、F如图2.
,垂足为E、F如图2.
∵ 平分
平分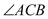 ,
, 、
、 ,垂足为E、F,
,垂足为E、F,
∴ .
.
又∵  ,∴
,∴  ≌
≌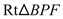 .┄┄┄┄┄┄┄┄4分
.┄┄┄┄┄┄┄┄4分
∴  .
.
∵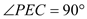 ,
,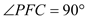 ,
, ,
,
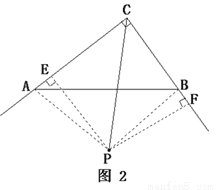 ∴
∴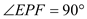 , 从而
, 从而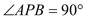 .
.
又 ∴
∴ 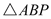 是等腰直角三角形. ┄┄┄┄┄┄┄┄5分
是等腰直角三角形. ┄┄┄┄┄┄┄┄5分
(2)如图2,在 中,
中,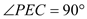 ,
,
 ,
,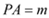 . ∴
. ∴ .
.
由 ≌
≌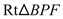 ,
,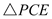 ≌
≌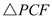 ,
,
可得 ,
, .
.
∴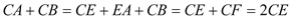 .
.
在 中,
中,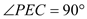 ,
,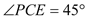 ,
, ,
,
∴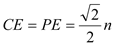 . ∴
. ∴ . ┄┄┄┄6分
. ┄┄┄┄6分
所以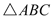 的周长为:
的周长为: . ┄┄┄┄7分
. ┄┄┄┄7分
因为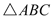 的面积=
的面积=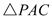 的面积
的面积
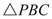 的面积
的面积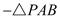 的面积
的面积
=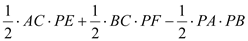 =
=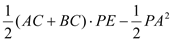
=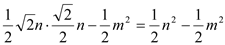 (
(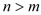 )┄┄9分
)┄┄9分
或 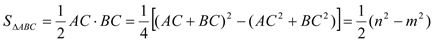 .
.
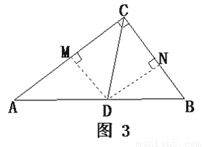
(3)过点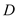 分别作
分别作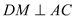 、
、 ,垂足为
,垂足为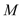 、
、 如图3.
如图3.
 ∵
∵ 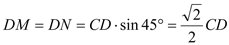 .┄┄┄┄10分
.┄┄┄┄10分
由 ∥
∥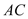 得
得 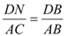 ①┄┄┄┄┄┄┄┄11分
①┄┄┄┄┄┄┄┄11分
由 ∥
∥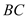 得
得 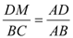 ② ┄┄┄┄┄┄12分
② ┄┄┄┄┄┄12分
①+②,得 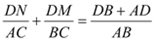 ,即
,即 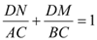 .
.
∴ 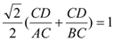 , 即
, 即 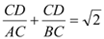 ┄┄┄┄13分
┄┄┄┄13分
【点睛】(1)由题意作出∠ACB的角平分线和线段AB的垂直平分线可求出点P,然后证明Rt△APE≌Rt△BPF即可;
(2)由PA=PB,PA=m,可得出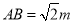 ,由Rt△APE≌Rt△BPF,△PCE≌△PCF,可得CA+CB=CE+EA+CB=CE+CF=2CE,在Rt△PCE中, PC=n,可知
,由Rt△APE≌Rt△BPF,△PCE≌△PCF,可得CA+CB=CE+EA+CB=CE+CF=2CE,在Rt△PCE中, PC=n,可知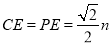 ,即
,即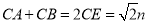 ,最后求出周长和面积;
,最后求出周长和面积;
(3)由平行线分线段成比例定理得到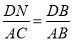 ,
, 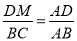 是解答本题的关键.
是解答本题的关键.
【题型】解答题
【结束】
15
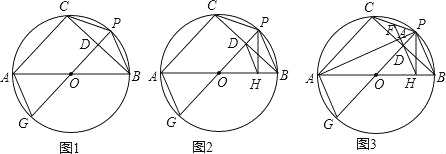
⊙O是△ABC的外接圆,AB是直径,过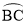 的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
(1)如图1,求证:AG=CP;
(2)如图2,过点P作AB的垂线,垂足为点H,连接DH,求证:DH∥AG;
(3)如图3,连接PA,延长HD分别与PA、PC相交于点K、F,已知FK=2,△ODH的面积为2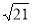 ,求AC的长.
,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com