
二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴是直线x=1,有以下四个结论:
①abc>0;②b2-4ac>0;③b=-2a;④a+b+c>2.其中正确的是______(填写序号)
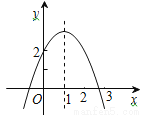
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期中测试 题型:解答题
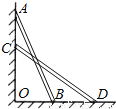
如图,一架长2.5m的梯子,斜靠在一竖直的墙上,这时,梯底距墙底端0.7m,如果梯子的顶端沿墙下滑0.4m,则梯子的底端将滑出多少米?
查看答案和解析>>
科目:初中数学 来源:青海省2017-2018学年七年级上学期12月月考数学试卷 题型:解答题
解方程: 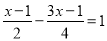
查看答案和解析>>
科目:初中数学 来源:青海省2017-2018学年七年级上学期12月月考数学试卷 题型:单选题
比-3小1的数是 ( )
A. 2 B. -2 C. 4 D. -4
D 【解析】试题解析:-3-1=-4. 故选D.查看答案和解析>>
科目:初中数学 来源:甘肃省定西市安定区2017-2018学年九年级上学期期末考试数学试卷 题型:解答题
已知二次函数当x=-1时,有最小值-4,且当x=0时,y=-3,求二次函数的表达式.
y=x2+2x-3 【解析】试题分析:由于已知抛物线与x轴的交点坐标,则可设顶点式y=a(x+1)2﹣4,然后把(0,3)代入求出a的值即可. 试题解析:设y=a(x+1)2﹣4 则﹣3=a(0+1)2﹣4 ∴a=1, ∴抛物线的解析式为y=(x+1)2﹣4 即:y=x2+2x﹣3.查看答案和解析>>
科目:初中数学 来源:甘肃省定西市安定区2017-2018学年九年级上学期期末考试数学试卷 题型:填空题
若二次函数y=-x2-4x+k的最大值是9,则k=______.
5 【解析】y=?(x?2)2+4+k, ∵二次函数y=?x2?4x+k的最大值是9, ∴4+k=9,解得:k=5, 故答案为:5.查看答案和解析>>
科目:初中数学 来源:甘肃省定西市安定区2017-2018学年九年级上学期期末考试数学试卷 题型:单选题
抛物线y=x2-8x-1的对称轴为( )
A. 直线x=4 B. 直线x=-4 C. 直线x=8 D. 直线x=-8
A 【解析】试题分析:先把抛物线解析式配成顶点式为y=(x-4)2-17, 所以抛物线的对称轴为x=4. 故选A.查看答案和解析>>
科目:初中数学 来源:江苏省东台市第三教育联盟2017-2018学年度第一学期第三次阶段检测七年级数学试卷 题型:填空题
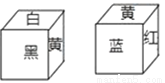
如图,下面两个正方体的六个面都按相同规律涂有红、黄、蓝、白、黑、绿六种颜色,那么黄色的对面是_________.
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 大题易丢分 题型:解答题
问题背景
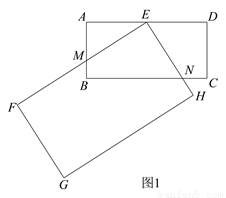
在数学活动课上,张老师要求同学们拿两张大小不同的矩形纸片进行旋转变换探究活动.如图 1,在矩形纸片ABCD 和矩形纸片EFGH中,AB=1,AD=2,且FE>AD,FG>AB,点E 是 AD 的中点,矩形纸片 EFGH 以点E 为旋转中心进行逆时针旋转,在旋转过程中会产生怎样的数量关系,提出恰当的数学问题并加以解决.
解决问题
下面是三个学习小组提出的数学问题,请你解决这些问题.
(1)“奋进”小组提出的问题是:如图 1,当 EF 与 AB 相交于点 M,EH 与 BC 相交于点 N 时,求证:EM=EN.
(2)“雄鹰”小组提出的问题是:在(1)的条件下,当 AM=CN 时,AM 与 BM 有怎样的数量关系,请说明理由.
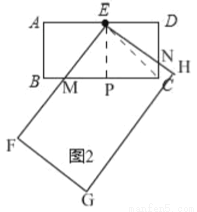
(3)“创新”小组提出的问题是:若矩形 EFGH 继续以点 E 为旋转中心进行逆时针旋转,当  时,请你在图 2 中画出旋转后的示意图,并求出此时 EF 将边 BC 分成的两条线段的长度.
时,请你在图 2 中画出旋转后的示意图,并求出此时 EF 将边 BC 分成的两条线段的长度.

【答案】(1)证明见解析;(2)AM=BN;(3)EF 将边 BC 分成的两条线段的长度为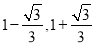 .
.
【解析】试题分析:(1)过点 E 作 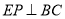 ,垂足为点P,根据已知条件证出PE=AE,再证得∠PEN=∠AEM,进而得到△PEN≌△AEM,即可证得结论;(2)易证PN=CN=
,垂足为点P,根据已知条件证出PE=AE,再证得∠PEN=∠AEM,进而得到△PEN≌△AEM,即可证得结论;(2)易证PN=CN= 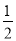 PC,进而求出PN=CN=
PC,进而求出PN=CN=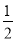 ,再判断出AM=PN=
,再判断出AM=PN=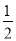 ,即可得出BM=
,即可得出BM=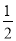 ,从而证得结论;(3)在Rt△PEM中,求出PM的长,再用线段的和差即可得出结论.
,从而证得结论;(3)在Rt△PEM中,求出PM的长,再用线段的和差即可得出结论.
试题解析:
(1) 如图1,过点 E 作 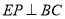 ,垂足为点 P,
,垂足为点 P,
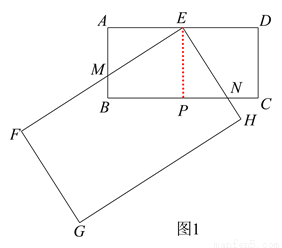
则四边形 ABPE 是矩形,∴PE=AB=1, 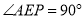 ,
,
∵ 点 E 是 AD 的中点,∴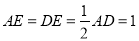 ,∴PE=AE,
,∴PE=AE,
∵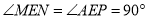 ,∴
,∴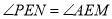 ,
,
∵PE=AE, 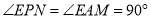 ,∴
,∴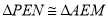 ,∴EM=EN.
,∴EM=EN.
(2) 由(1)知, 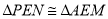 ,∴AM=PN,
,∴AM=PN,
∵AM=CN,∴PN=CN=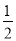 PC,
PC,
∵ 四边形 EPCD 是矩形,∴PC=DE=1,PN=CN=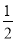 ,
,
∴AM=PN=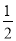 ,BM=AB-AM=
,BM=AB-AM=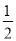 ,∴AM=BN.
,∴AM=BN.
(3)如图2,当∠AEF=60°时,
设EF与BC交于M,EH与CD交于N,过点E作EP⊥BC于P,连接EC,
由(1)知,CP=EP=1,AD∥BC,
∴∠EMP=∠AEF=60°,
在Rt△PEM中,PM=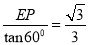 ,
,
∴BM=BP﹣PM=1﹣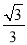 ,CM=PC+PM=1+
,CM=PC+PM=1+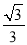 ,
,
∴EF将边BC分成的两条线段的长度为1﹣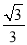 ,1+
,1+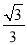 .
.
【题型】解答题
【结束】
20
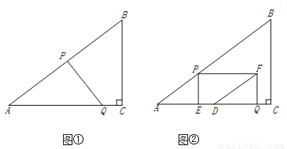
如图①,在Rt△ABC中,∠C=90°,AB=10,BC=6.点P从点A出发,沿折现AB—BC向终点C运动,在AB上以每秒5个单位长度的速度运动,在BC上以每秒3个单位长度的速度运动.点Q从点C出发,沿CA方向以每秒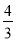 个单位长度的速度运动.点P、Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
个单位长度的速度运动.点P、Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
(1)求线段AQ的长.(用含t的代数式表示)
(2)当PQ与△ABC的一边平行时,求t的值
(3)如图②,过点P作PE⊥AC于点E,以PE、QE为邻边作矩形PEQF,点D为AC的中点,连结DF.直接写出DF将矩形PEQF分成两部分的面积比为1:2时t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com