练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

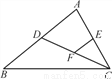
    如图，CD是△ABC的中线，点E，F分别是AC，DC的中点，EF＝1，则BD＝____________.

    2 【解析】∵点E.F分别是AC、DC的中点，∴EF是△ADC的中位线，∴EF=AD，∵EF=1，∴AD=2， ∵CD是△ABC的中线，∴BD=AD=2，故答案为：2.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：黄金30题系列 九年级数学 小题好拿分 题型：单选题

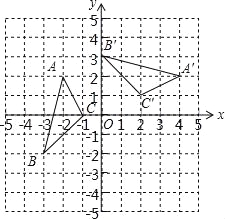
    如图，在平面直角坐标系中，△ABC绕某一点P旋转一定的角度得到△A′B′C′，根据图形变换前后的关系可得点P的坐标为（ ）.

    A．（0，1） B．（1，﹣1） C．（0，﹣1） D．（1，0）

    B． 【解析】 试题分析：根据网格结构，找出对应点连线的垂直平分线的交点即为旋转中心．由图形可知，对应点的连线CC′、AA′的垂直平分线的交点是点（1，﹣1），根据旋转变换的性质，点（1，﹣1）即为旋转中心． 故旋转中心坐标是P（1，﹣1）．故选B．

    查看答案和解析>>

    科目：初中数学 来源：2017年广东省东莞市堂星晨学校考数学模拟试卷 题型：解答题

    解不等式组： ．

    ﹣≤x＜1 【解析】试题分析：根据不等式的性质化简并计算每个不等式的取值范围，然后求两个范围的交集即可. 试题解析：解不等式2x＜，得：x＜1， 解不等式3（x+1）≥x+2，得：x≥﹣， 则不等式组的解集为﹣≤x＜1．

    查看答案和解析>>

    科目：初中数学 来源：2017年广东省东莞市堂星晨学校考数学模拟试卷 题型：单选题

    在﹣1、0、1、2这四个数中，最小的数是（　　）

    A. ﹣1 B. 0

    C. 1 D. 1

    A 【解析】∵-1<0<1<2； ∴最小的数是－1。 故选A。

    查看答案和解析>>

    科目：初中数学 来源：2018年春人教版八年级数学下册（广西）期中测试 题型：解答题

    已知：如图，点P是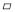ABCD的对角线AC的中点，经过点P的直线EF交AB于点E，交DC于点F.求证：AE＝CF.

    见解析 【解析】试题分析：由四边形是平行四边形，易得点是的中点，可得又由对顶角相等，可得即可利用证得即可证得 试题解析：∵四边形是平行四边形， 又∵点是的中点， 在和中，

    查看答案和解析>>

    科目：初中数学 来源：2018年春人教版八年级数学下册（广西）期中测试 题型：单选题

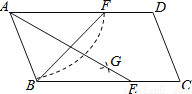
    如图，在平行四边形ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E，若BF=12，AB=10，则AE的长为（ ）

    A．16 B．15 C．14 D．13

    A 【解析】 试题分析：首先证明四边形ABEF是菱形，得出AE⊥BF，OB=OF=6，OA=OE，利用勾股定理计算出AO，从而得到AE的长． 【解析】 连结EF，AE与BF交于点O，如图， ∵AO平分∠BAD， ∴∠1=∠2， ∵四边形ABCD为平行四边形， ∴AF∥BE， ∴∠1=∠3， ∴∠2=∠3， ∴AB=EB， 同理：A...

    查看答案和解析>>

    科目：初中数学 来源：2018年春人教版八年级数学下册（广西）期中测试 题型：单选题

    关于?ABCD的叙述，正确的是（　　）

    A. 若AB⊥BC，则?ABCD是菱形 B. 若AC⊥BD，则?ABCD是正方形

    C. 若AC=BD，则?ABCD是矩形 D. 若AB=AD，则?ABCD是正方形

    C 【解析】选项C中，满足矩形的判定定理：对角线相等的平行四边形是矩形，所以选C.

    查看答案和解析>>

    科目：初中数学 来源：青海省2017-2018学年七年级上学期12月月考数学试卷 题型：解答题

    某文艺团体为“希望工程”募捐组织了一场义演，共售出1000张票，筹出票款6920元，且每张成人票8元，学生票5元．

    （1）问成人票与学生票各售出多少张？

    （2）若票价不变，仍售出1000张票，所得的票款可能是7290元吗？为什么？

    （1）成人票640张，学生票360张；（2）不可能，理由见解析． 【解析】 试题分析：（1）设成人票x张，则学生票（1000－x）张，根据题意列出方程进行求解，得出答案；（2）设成人票y张，则学生票（1000－y）张，然后根据题意列出方程求出y的值，看y是否为整数，如果是整数则符合条件，如果不是整数则不符合条件． 试题解析：（1）设售出的成人票为x张，根据题意得：8x+5（100...

    查看答案和解析>>

    科目：初中数学 来源：甘肃省定西市安定区2017-2018学年九年级上学期期末考试数学试卷 题型：单选题

    如图，已知AB是⊙O的直径，∠D=40°，则∠CAB的度数为( )

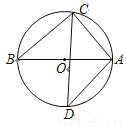
    A. 20° B. 40° C. 50° D. 70°

    C 【解析】∵∠D=40°， ∴∠B=∠D=40°. ∵AB是O的直径， ∴∠ACB=90°， ∴∠CAB=90°?40°=50°. 故选：C.

    查看答案和解析>>

    同步练习册答案