练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

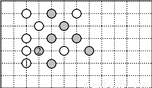
    同学们玩过五子棋吗？它的比赛规则是只要同色5子先成一条直线就算胜，如图是两人玩的一盘棋，若白①的位置是(1，－5)，黑②的位置是(2，－4)，现轮到黑棋走，你认为黑棋放在_______位置就可获胜．

    (2,0)或（7，-5） 【解析】由白①的位置是(1，－5)，黑?的位置是(2，－4)，则可知白①是从如图中的点O开始向右一格再向下5格得到；黑①是从图中的点O开始向右2格再向下4格得到.由黑棋放在图中黑②或黑③处都可以获胜，黑②是从点O开始向右2格得到，即用（2，0）表示；黑③是从点O开始向右7格再向下5格得到，即用（7，-5）表示. 故答案为(2，0)或(7，－5).
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版数学七年级上册 第四章 基本平面图形练习题 题型：解答题

    比较两个角的大小，有以下两种方法(规则)：①用量角器度量两个角的大小，用度数表示，则角度大的角大；②构造图形，如果一个角包含(或覆盖)另一个角，则这个角大．对于下图给定的∠ABC与∠DEF，用以上两种方法分别比较它们的大小．注：构造图形时，作示意图(草图)即可．

    ∠DEF＞∠ABC. 【解析】方法一:测量∠ABC= 45、∠DEF=65，所以∠ABC>∠DEF 方法二：使∠ABC得一边BC与∠DEF的一边EF重合，BA落在∠DEF的内部，所以∠ABC>∠DEF

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级上册 第四章 基本平面图形练习题 题型：单选题

    把弯曲的河道改直，能够缩短航程，这样做的道理是（ ）

    A. 两点之间，射线最短 B. 两点确定一条直线

    C. 两点之间，线段最短 D. 两点之间，直线最短

    C 【解析】试题分析：将曲线改成直线能缩短距离是因为两点之间线段最短.

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级上册 第四章 基本平面图形练习题 题型：单选题

    如图，点A、B、C是直线l上的三个点，图中共有线段条数是（　　）

    A. 1条 B. 2条 C. 3条 D. 4条

    C 【解析】【解析】 图中线段有：线段AB、线段AC、线段BC，共三条．故选C．

    查看答案和解析>>

    科目：初中数学 来源：2018年春人教版七年级数学下册期中测试 题型：解答题

    小丽想用一块面积为900 cm2的正方形纸片，沿着边的方向裁出一块面积为600 cm2的长方形纸片，使它的长宽之比为4∶3，她不知道是否裁得出来，正在发愁，小明见了说：“别发愁，一定能用这块正方形纸片裁出需要的长方形纸片．”你同意小明的说法吗？小丽能用这块纸片裁出符合要求的纸片吗？

    见解析 【解析】试题分析：根据算术平方根的概念求出正方形的边长，根据长方形纸片的面积求出边长，计算比较得到答案． 试题解析：同意小明的说法． 面积为900 cm2的正方形纸片的边长为30 cm.设长方形的长为4x cm，宽为3x cm，根据边长与面积的关系得4x×3x＝600.解得x＝.因此长方形纸片的长为4cm. ∵＜7.5， ∴4＜30. ∴小丽能用这块纸片...

    查看答案和解析>>

    科目：初中数学 来源：2018年春人教版七年级数学下册期中测试 题型：填空题

    命题“两直线平行，内错角相等”的题设是_________，结论_________．

    两直线平行 内错角相等 【解析】试题分析：命题由题设和结论两部分组成．题设是已知事项，结论是由已知事项推出的事项．命题常常可以写为“如果…那么…”的形式，如果后面接题设，而那么后面接结论． 【解析】 题设：如果两条平行线被第三条直线所截；结论：那么内错角相等．

    查看答案和解析>>

    科目：初中数学 来源：2018年春人教版七年级数学下册期中测试 题型：单选题

    若将点A(1，3)向左平移2个单位，再向下平移4个单位得到B，则点B的坐标为( )

    A. (－2，－1) B. (－1，0) C. (－1，－1) D. (－2，0)

    C 【解析】∵点A（1，3）向左平移2个单位，再向下平移4个单位得到点B， ∴点B的横坐标为1?2＝?1，纵坐标为3?4＝?1， ∴B的坐标为（?1，?1）． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：山东省诸城市2018届九年级上期末模拟数试卷 题型：填空题

    如图，在?ABCD中，AB=6，BC=8，∠C的平分线交AD于E，交BA的延长线于F，则AF的长为________．

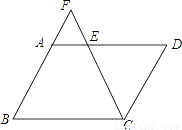
    2 【解析】试题分析：∵四边形ABCD是平行四边形， ∴AD∥BC，AD＝BC＝8， ∴∠F＝∠FCD， ∵CE平分∠BCD， ∴∠BCE＝∠FCD， ∴∠F＝∠BCE， ∴BF＝BC＝6， ∴AF＝BF－AB＝8－6＝2； 故答案为：2．

    查看答案和解析>>

    科目：初中数学 来源：甘肃省定西市安定区2016-2017学年八年级上学期期末考试数学试卷 题型：解答题

    如图，在△ABC中，AB＝CB，∠ABC＝90°，D为AB延长线上一点，点E在BC边上，且BE＝BD，连结AE、DE、DC．

    ① 求证：△ABE≌△CBD；

    ② 若∠CAE＝30°，求∠BDC的度数．

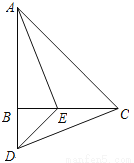
    ①证明见解析②∠BDC＝75° 【解析】试题分析：（1）利用“边角边”证明△ABE≌△CBD即可；②先根据等腰直角三角形的锐角都是45°求出∠CAB，再求出∠BAE，然后根据全等三角形对应角相等求出∠BCD，再根据直角三角形两锐角互余其解即可； 试题解析： （1）证明：∵∠ABC=90°，D为AB延长线上一点， ∴∠ABE=∠CBD=90°， 在△ABE和△CBD中，...

    查看答案和解析>>

    同步练习册答案