
科目:初中数学 来源:湖北省黄冈市2017-2018学年八年级(上)期中数学试 题型:单选题
如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC交AB于点E,则有( )
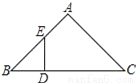
A. DE=DB B. DE=AE C. AE=BE D. AE=BD
B 【解析】试题解析:连接 在和中, ∴≌(HL), 故B选项正确; 在中, ,即,故C选项错误; 根据已知不能得出,故A选项错误; 根据已知不能得出,由,即不能推出,故D选项错误. 故选B.查看答案和解析>>
科目:初中数学 来源:江苏省2017-2018学年七年级上学期第二次月考数学试卷 题型:填空题
如图,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行.若甲的速度是乙的速度的3倍,则它们第2018次相遇在___边上.
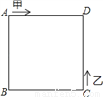
查看答案和解析>>
科目:初中数学 来源:北京市2018届九年级(上)期中数学试卷 题型:解答题
如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O交CA于点E,点G是AD的中点.
(1)求证:GE是⊙O的切线;
(2)若AC⊥BC,且AC=8,BC=6,求切线GE的长.
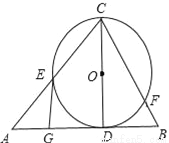
查看答案和解析>>
科目:初中数学 来源:北京市2018届九年级(上)期中数学试卷 题型:填空题
已知关于x的二次函数y=ax2+(a2﹣1)x﹣a的图象与x轴的一个交点的坐标为(m,0),若3<m<4,则a的取值范围是_____.
<a<或﹣4<a<﹣3 【解析】∵y=ax2+(a2﹣1)x﹣a=(ax﹣1)(x+a), ∴当y=0时,可解得:x1=,x2=﹣a, ∴抛物线与x轴的交点为(,0)和(﹣a,0). ∵抛物线与x轴的一个交点的坐标为(m,0)且2<m<3, ∴(1)当a>0时,3<<4,解得; (2)当a<0时,3<﹣a<4,解得﹣4<a<﹣3. 综上所述,a的取值范围是...查看答案和解析>>
科目:初中数学 来源:北京市2018届九年级(上)期中数学试卷 题型:单选题
已知正六边形的边长为3,则这个正六边形的半径是( )
A. 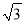 B. 2
B. 2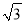 C. 3 D. 3
C. 3 D. 3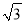
查看答案和解析>>
科目:初中数学 来源:辽宁省大连市沙河口区孙家沟九年制学校2018届九年级(上)期中数学试卷 题型:解答题
已知抛物线y=ax2+bx+c 如图所示,直线x=-1是其对称轴,

(1)确定a,b,c, Δ=b2-4ac的符号,
(2)求证:a-b+c>0,
(3)当x取何值时,y>0;当x取何值时y<0.
(1)a<0,b<0,c>0,b2-4ac>0; (2)a-b+c>0; (3)当-3查看答案和解析>>
科目:初中数学 来源:辽宁省大连市沙河口区孙家沟九年制学校2018届九年级(上)期中数学试卷 题型:单选题
如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕B点按顺时针方向转动一个角度到A1BC1的位置,使得点A,B,C1在同一条直线上,那么这个角度等于( ).
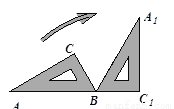
A. 120° B. 90° C. 60° D. 30°
A 【解析】试题分析:根据旋转图形的性质可得:旋转的角度为180°-60°=120°.查看答案和解析>>
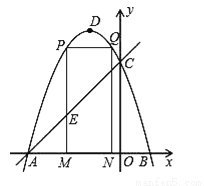
科目:初中数学 来源:湖北省武汉市江夏区2018届九年级上期末模拟数学试卷 题型:解答题
如图,抛物线y=﹣x2﹣2x+3的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求点A、B、C的坐标;
(2)点M(m,0)为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,可得矩形PQNM.如图,点P在点Q左边,试用含m的式子表示矩形PQNM的周长;
(3)当矩形PQNM的周长最大时,m的值是多少?并求出此时的△AEM的面积;
(4)在(3)的条件下,当矩形PMNQ的周长最大时,连接DQ,过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=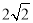 DQ,求点F的坐标.
DQ,求点F的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com