
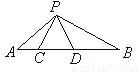
如图,点 C 、 D在线段 AB上,△ PCD是等边三角形.①当 AC 、 CD 、 DB满足怎样的关系时△ ACP∽△ PDB;②当△ ACP∽△ PDB时,求∠ APB.
科目:初中数学 来源:北师大版八年级下册数学第五章分式与分式方程单元检测卷 题型:单选题
化简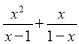 的结果是( )
的结果是( )
A. x+2 B. x﹣1 C. ﹣x D. x
D 【解析】【解析】 原式= .故选D.查看答案和解析>>
科目:初中数学 来源:安徽省阜阳市颍上县十校联考2017-2018学年度八年级第一学期期末考试数学试卷(沪科) 题型:单选题
如图,ΔABC中,以B为圆心,BC长为半径画弧,分别交AC、AB于D、E两点,并连接BD、DE.若∠A=30°,AB=AC,则∠BDE的度数为( )
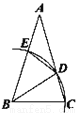
A. 67.5° B. 52.5° C. 45° D. 75°
A 【解析】根据AB=AC,利用三角形内角和定理求出∠ABC的度数,再利用等腰三角形的性质和三角形内角和定理求出∠DBC=30°,然后即可求出∠BDE的度数. 【解析】 ∵AB=AC, ∴∠ABC=∠ACB, ∵∠A=30°, ∴∠ABC=∠ACB=(180°﹣30°)=75°, ∵以B为圆心,BC长为半径画弧, ∴BE=BD=BC, ∴∠BDC=...查看答案和解析>>
科目:初中数学 来源:人教版七年级下册数学 全册综合测试卷 题型:单选题
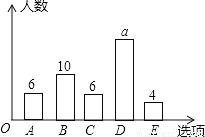
为了解中学生获取资讯的主要渠道,设置“A:报纸,B:电视,C:网络,D:身边的人,E:其他”五个选项(五项中必选且只能选一项)的调查问卷,先随机抽取50名中学生进行该问卷调查,根据调查的结果绘制条形图如图所示,该调查的方式是( ),图中的a的值是( )
 v
v
A.全面调查,26 B.全面调查,24 C.抽样调查,26 D.抽样调查,24
D 【解析】 根据关键语句“先随机抽取50名中学生进行该问卷调查,”可得该调查方式是抽样调查,调查的样本容量为50,故6+10+6+a+4=50,解即可. 【解析】 该调查方式是抽样调查, a=50﹣6﹣10﹣6﹣4=24, 故选:D.查看答案和解析>>
科目:初中数学 来源:人教版七年级下册数学 全册综合测试卷 题型:单选题
规定用符号[m]表示一个实数m的整数部分,例如:[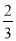 ]=0,[3.14]=3.按此规定[
]=0,[3.14]=3.按此规定[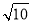 +1]的值为( )
+1]的值为( )
A.3 B.4 C.5 D.6
B 【解析】 试题分析:根据,则,即,根据题意可得:=4.查看答案和解析>>
科目:初中数学 来源:2017-2018学年度人教版九年级数学下册第27 章同步课时练习:27.2.1 相似三角形的判定(第2课时) 题型:填空题
如图,△ ABC中 CD为高线, AD=4, CD=3,则当 DB= _______时,△ ADC∽△ CDB.
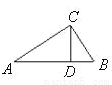
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度人教版九年级数学下册第26 章同步课时练习:26.2 实际问题与反比例函数(第1课时) 题型:解答题
一辆汽车往返于甲、乙两地之间,如果汽车以50千米/时的平均速度从甲地出发,则经过6小时可到达乙地.
(1)甲、乙两地相距多少千米?
(2)如果汽车把速度提高到 v(千米/时),那么从甲地到乙地所用时间 t(小时)将怎样变化?
(3)写出 t与 v之间的函数关系式;
(4)因某种原因,这辆汽车需在5小时内从甲地到达乙地,则此时汽车的平均速度至少应是多少?
(5)已知汽车的平均速度最大可达80千米/时,那么它从甲地到乙地最快需要多长时间?
(1) 300千米;(2) t将减小;(3) t= ( v>0);(4) v≥60千米/时;(5) t=3.75小时. 【解析】试题分析:(1)用速度乘以时间即可求得路程; (2)根据路程、速度及时间之间的关系说明即可; (3)写出函数关系式即可; (4)用路程除以时间即可求得速度,从而得到答案. (5)用路程除以速度即可求得时间,从而得到答案. 试题解析:(1...查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学人教版上册 第14章 整式的乘法与因式分解 单元测试 题型:填空题
已知2a2+2b2=10,a+b=3,则ab=________.
2 【解析】∵2a2+2b2=10, ∴a2+b2=5. ∵a+b=3, ∴(a+b)2=32, ∴a2+2ab+b2=9, ∴2ab=4, ∴ab=2.查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学人教版下册16.1二次根式 同步练习 题型:解答题
若x,y为实数,且y=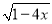 +
+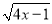 +
+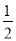 .求
.求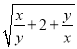 -
-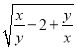 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com