
如图,直线y=ax+b过点A(0,2)和点B(﹣3,0),则方程ax+b=0的解是( )

A. x=2 B. x=0 C. x=﹣1 D. x=﹣3
D 【解析】∵方程ax+b=0的解是直线y=ax+b与x轴的交点横坐标, ∴方程ax+b=0的解是x=-3. 故选D.科目:初中数学 来源:山东省德州地区2017-2018学年度七年级第一学期期末检测数学试卷 题型:单选题
北京某天的最高气温是10℃,最低气温是 -2℃,则这两天的温差是( )
A. 12℃ B. -12℃ C. 8℃ D. -8℃
A 【解析】试题分析:温差=最高气温-最低气温 =10-(-2) =10+2 =12(℃). 故选A.查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十六章达标检测卷 题型:填空题
x,y分别为8-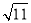 的整数部分和小数部分,则2xy-y2=____________.
的整数部分和小数部分,则2xy-y2=____________.
查看答案和解析>>
科目:初中数学 来源:2018届中考数学专题复习同步练习题:一次函数 题型:解答题
直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).
(1)求直线AB的解析式;
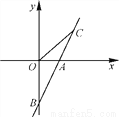
(2)若直线AB上一点C在第一象限且点C的坐标为(2,2),求△BOC的面积.
(1) y=2x-2(2)2 【解析】试题分析:(1)设直线AB的解析式为 将点点分别代入解析式即可组成方程组,从而得到AB的解析式; (2)以OB为底边,C到OB的垂线段为高,根据三角形的面积公式即可求解. 试题解析:(1)设直线AB的解析式为y=kx+b(k≠0), ∵直线AB过点A(1,0)、点B(0,?2), ∴ 解得 ∴直线AB的解析式为y=2x?2; ...查看答案和解析>>
科目:初中数学 来源:2018届中考数学专题复习同步练习题:一次函数 题型:填空题
在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1 ______ y2.(填“>”“<”或“=”)
< 【解析】试题解析:∵一次函数y=2x+1中k=2>0, ∴y随x的增大而增大, ∵x1<x2, ∴y1<y2.查看答案和解析>>
科目:初中数学 来源:2017-2018学年人教版七年级数学第五章相交线与平行线单元测试 题型:解答题
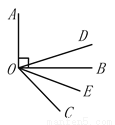
如图,DO平分∠AOC,OE平分∠BOC,若OA⊥OB,
(1)当∠BOC=30°,∠DOE=_______________; 当∠BOC=60°,∠DOE=_______________;
(2)通过上面的计算,猜想∠DOE的度数与∠AOB有什么关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年人教版七年级数学第五章相交线与平行线单元测试 题型:填空题
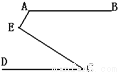
如图,AB∥CD,∠BAE = 120º,∠DCE = 30º,则∠AEC = _______度.
查看答案和解析>>
科目:初中数学 来源:人教版初中数学九年级上册第二十一章《配方法解一元二次方程》练习题 题型:填空题
若方程x2-m=0有整数根,则m的值可以是_______________(只填一个)
1(答案不唯一) 【解析】【解析】 若方程x2-m=0有整数根,则x=±,只要m为正整数,且m是完全平方数即可.故m可以取1.故答案为:1(答案不唯一).查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:期末达标检测卷 题型:填空题
某市为鼓励市民节约用水和加强对节水的管理,制订了以下每月每户用水的收费标准:(1)用水量不超过8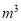 时,每立方米收费1元;(2)超出8
时,每立方米收费1元;(2)超出8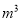 时,在(1)的基础上,超过8
时,在(1)的基础上,超过8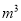 的部分,每立方米收费2元.设某户一个月的用水量为
的部分,每立方米收费2元.设某户一个月的用水量为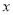
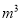 ,应交水费
,应交水费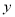 元. 则当
元. 则当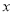 >8时,
>8时, 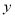 关于
关于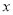 的函数解析式是_______.
的函数解析式是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com