
如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判定△ADE与△ABC相似的是( )
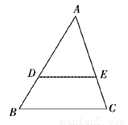
A. 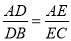 B.
B. 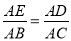
C. 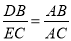 D.
D. 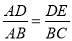
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型:填空题
若一元二次方程x2-x-1=0的两根分别为x1,x2,则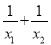 = .
= .
【答案】-1
【解析】∵一元二次方程: 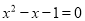 的两根是
的两根是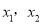 ,
,
∴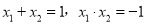 ,
,
∴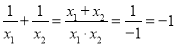 .
.
点睛:不解方程,求含有一元二次方程两根的代数式的值时,通常分两步完成:(1)由方程得到: 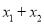 、
、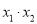 的值(前提是“根的判别式△
的值(前提是“根的判别式△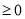 ”);(2)把要求值的代数式变形为用含“
”);(2)把要求值的代数式变形为用含“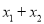 ”和“
”和“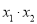 ”表达的形式,再代值计算即可.
”表达的形式,再代值计算即可.
【题型】填空题
【结束】
12
已知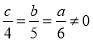 ,则
,则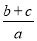 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源:初一数学第一学期5.2.3去分母解一元一次方程 同步练习 题型:解答题
解方程: 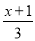 +1=x﹣
+1=x﹣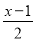 .
.
查看答案和解析>>
科目:初中数学 来源:安徽省合肥市西校2018届九年级上学期期中考试数学试卷 题型:解答题
有一辆载有长方体形状集装箱的货车想通横截面为抛物线的隧道,如图所示,已知隧道底部宽AB为 4 m,高OC为 3.2 m,集装箱的宽与货车的宽都是 2.4 m,集装箱顶部离地面 2.1 m.这辆货车能通过这个隧道吗?请说明理由.
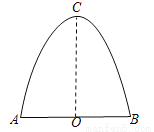
查看答案和解析>>
科目:初中数学 来源:安徽省合肥市西校2018届九年级上学期期中考试数学试卷 题型:填空题
已知A(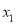 ,
, 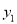 )和B(
)和B(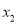 ,
, 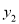 )是反比例函数
)是反比例函数 的图象上两点,若
的图象上两点,若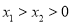 ,则y1与y2的大小关系是________.
,则y1与y2的大小关系是________.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型:解答题
如图,已知四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
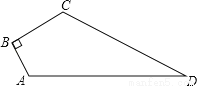
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型:单选题
已知△ABC的三边分别长为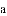
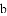
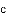
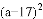 +
+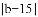 +
+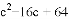 =0,则△ABC是( ).
=0,则△ABC是( ).
A. 以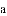
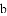
C. 以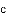
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 第24章小结与复习 练习 题型:解答题
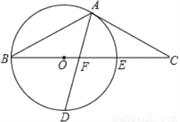
如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,AC=FC.
(1)求证:AC是⊙O的切线;
(2)已知圆的半径R=5,EF=3,求DF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com