
若n为正整数,那么(-1) n a +(-1) n+1a化简的结果是( )
A. 0 B. 2a C. -2a D. 2a或-2a
A 【解析】试题解析:当正整数是奇数时,对进行运算,得 当正整数是偶数时,对进行运算,得 故选A.科目:初中数学 来源:安徽省巢湖市2016~17学年度第一学期 期末教学质量检测 八年级数学试卷 题型:解答题
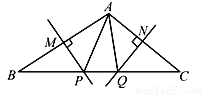
如图所示,MP和NQ分别垂直平分AB和AC.
(1)若△APQ的周长为12,求BC的长;
(2)∠BAC=105°,求∠PAQ的度数.
查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年七年级数学上期末复习检测数学试卷 题型:单选题
下列计算结果中等于3的数是( )
A. |﹣7|+|+4| B. |(﹣7)+(+4)| C. |+7|+|﹣4| D. |(﹣7)﹣(﹣3)|
B 【解析】A. |﹣7|+|+4|=7+4=11,不符合题意;B. |(﹣7)+(+4)| =3,符合题意;C. |+7|+|﹣4| =7+4=11,不符合题意;D. |(﹣7)﹣(﹣3)|=|-7+3|=4,不符合题意, 故选B.查看答案和解析>>
科目:初中数学 来源:黑龙江省2017-2018学年七年级数学上学期期末试卷 题型:填空题
方程(a-2)x|a|-1+3=0是关于x的一元一次方程,则a=____.
-2 【解析】试题解析:根据一元一次方程的定义,可得: 解得: 把代入方程得: 解得: 故答案为:查看答案和解析>>
科目:初中数学 来源:黑龙江省2017-2018学年七年级数学上学期期末试卷 题型:单选题
下列各组数中,相等的是( ).
A. –1与(–4)+(–3) B. 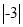 与–(–3) C.
与–(–3) C. 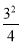 与
与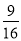 D.
D. 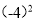 与–16
与–16
查看答案和解析>>
科目:初中数学 来源:宁夏2017-2018学年第一学期七年级上册数学期末试卷 题型:解答题
解方程:(1)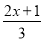 -
-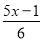 =1;(2)x-
=1;(2)x-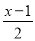 =2-
=2-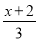 .
.
查看答案和解析>>
科目:初中数学 来源:宁夏2017-2018学年第一学期七年级上册数学期末试卷 题型:单选题
阳光公司销售一种进价为21元的电子产品,按标价的九折销售,仍可获利20%,则这种电子产品的标价为( )
A. 26元 B. 27元 C. 28元 D. 29元
C 【解析】试题分析:根据题意,设电子产品的标价为x元,按照等量关系“标价×0.9﹣进价=进价×20%”,列出一元一次方程得:0.9x﹣21=21×20%解得:x=28所以这种电子产品的标价为28元. 故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市九年级数学科期末检测题 题型:填空题
当x<3时,化简: 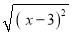 =_______.
=_______.
查看答案和解析>>
科目:初中数学 来源:湖北省襄阳市襄城区2016-2017学年度上学期期末考试九年级数学试卷 题型:解答题
如图,在平面直角坐标系中,抛物线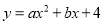 与坐标轴分别交于点A、点B、点C,并且∠ACB=90º,AB=10.
与坐标轴分别交于点A、点B、点C,并且∠ACB=90º,AB=10.
(1)求证:△OAC∽△OCB;
(2)求该抛物线的解析式;
(3)若点P是(2)中抛物线对称轴上的一个动点,是否存在点P使得△PAC为等腰三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.
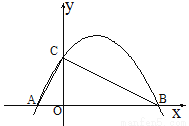
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com