
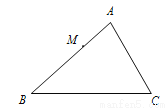
��ͼ���ڡ�ABC�У�AB��9��AC��6��BC��12����M�ڱ�AB�ϣ�AM��3������M��ֱ��MN���AC���ڵ�N��ʹ�صõ���������ԭ������ABC���ƣ���MN�ij�Ϊ_____��
 100�ִ�����ĩ���ϵ�д�
100�ִ�����ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�����������������ѧУ2017-2018ѧ��ȵ�һѧ�ڰ��꼶��ѧ�����Ծ� ���ͣ���ѡ��
��ͼ��B��D��E��C�ĵ㹲�ߣ��ҡ�ABD�ա�ACE������AEC=105�㣬���DAE�Ķ������ڣ���������

A. 30�� B. 40�� C. 50�� D. 65��
A ���������������� �ߡ�ABD�ա�ACE�����ADB=��AEC=105�㣬���ADE=��AED=75�㣬���DAE=180�㩁75�㩁75��=30�㣬��ѡA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ��Ҧ��2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
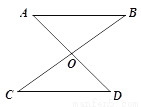
��֪����ͼ��ֱ��AD��BC���ڵ�O��OA=OD��OB=OC����֤��AB��CD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ͼ���������2016~2017ѧ��ȵ�һѧ���ھ��꼶�Ծ� ���ͣ������
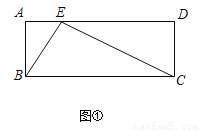
�ھ���ABCD�У�AB��4��BC��10��E��ֱ��AD������һ�㣨�����A�غϣ�����A����ֱ��BE�ĶԳƵ�ΪA�䣬AA������ֱ����ֱ��BC���ڵ�F��
��1����ͼ�٣�����E���߶�AD��ʱ��������ABE �ס�DEC����AE�ij���
����AE��x��BF��y����y��x�ĺ�������ʽ��
��2���߶�DA���ȡֵ��Χ�� ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ͼ���������2016~2017ѧ��ȵ�һѧ���ھ��꼶�Ծ� ���ͣ������
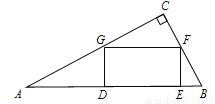
��ͼ����Rt��ABC�У���C��90�㣬����DEFG�Ķ���G��F�ֱ���AC��BC�ϣ�DE��AB�ϣ�
��1����֤����ADG�ס�FEB��
��2����AG��5��AD��4����BE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ͼ���������2016~2017ѧ��ȵ�һѧ���ھ��꼶�Ծ� ���ͣ������
��һ������1��2��x��3��4��ƽ������3�����������ݵļ�����________��
4 ������������һ������1��2��x��3��4��ƽ������3�� �� (1+2+x+4)=3 ��x=5�� �༫��=5?1=4 �ʴ�Ϊ��4.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ͼ���������2016~2017ѧ��ȵ�һѧ���ھ��꼶�Ծ� ���ͣ���ѡ��
����һö�ʵؾ��ȵ�����һ�Σ�����һ���������4�ĸ����ǣ�������
A. 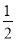 B.
B. 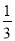 C.
C. 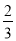 D.
D. 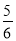
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ͼ�����ˮ��2016~2017ѧ��ȵ�һѧ����ĩ���꼶�Ծ� ���ͣ������
��ͼ����O�У���AOB��110�㣬��C��D�ǻ�AmB�������㣬���C����D�Ķ�����________�㣮
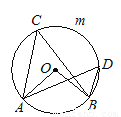
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�������ж�����2017-2018ѧ��ȵ�һѧ����ĩ��ѧĿ���������ѧ�Ծ� ���ͣ������
��֪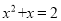 ����
����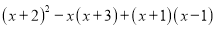 ��ֵ
��ֵ
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com