练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

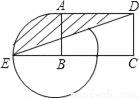
    如图，已知矩形ABCD中，AD=2AB=2，以B为圆心，BA为半径作圆弧交CB的延长线于E，则图中阴影部分的面积是　 　．

    +． 【解析】∵AD=2AB=2，∴AB=1， ∴S 阴影 =S 扇形ABE +S ?ABCD -S △DCE ==， 故答案为： .
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型：单选题

    下列三角形不一定全等的是（    ）

    A. 面积相等的两个三角形

    B. 周长相等的两个等边三角形

    C. 斜边和一条直角边分别对应相等的两个直角三角形

    D. 有一个角是100°，腰长相等的两个等腰三角形

    A 【解析】A、如果△ABC和△DEF中，BC=1，BC上的高AD=2，△DEF的边EF=2，EF上的高是1，两三角形的面积相等，但△ABC和△DEF不一定全等，故本选项正确； B、△ABC和△DEF，AB=BC=AC，DE=EF=DF，根据周长相等，则AB=BC=AC=DE=DF=EF，根据SSS即可推出两三角形全等，故本选项错误； C、根据直角三角形全等的判定定理HL，推出两...

    查看答案和解析>>

    科目：初中数学 来源：湖南省邵阳县黄亭市2017~2018学年九年级数学（上）期末综合检测模拟题 题型：解答题

    计算： ．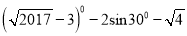

    －2 【解析】试题分析：先分别计算零次幂、特殊角三角函数以及算术平方根，再计算乘法，最后算加减法即可得出结果. 试题解析： = =-2.

    查看答案和解析>>

    科目：初中数学 来源：湖南省邵阳县黄亭市2017~2018学年九年级数学（上）期末综合检测模拟题 题型：单选题

    一元二次方程3x2 – 2x＝0的解是（　　）

    A. 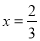B. x=0 C. x1= 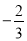，x2=0 D. x1= 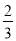，x2=0

    D 【解析】试题解析：x（3x-2）=0， x=0或3x-2=0， 所以x1=0，x2=． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省兰州市中考数学模拟试卷 题型：解答题

    如图1，一枚质地均匀的正四面体骰子，它有四个面并分别标有数字1，2，3，4．如图2，正方形ABCD顶点处各有一个圈．跳圈游戏的规则为：游戏者每掷一次骰子，骰子着地一面上的数字是几，就沿正方形的边顺时针方向连续跳几个边长．

    如：若从圈A起跳，第一次掷得3，就顺时针连续跳3个边长，落到圈D；若第二次掷得2，就从D开始顺时针连续跳2个边长，落到圈B；…

    设游戏者从圈A起跳．

    （1）嘉嘉随机掷一次骰子，求落回到圈A的概率P1；

    （2）淇淇随机掷两次骰子，用列表法求最后落回到圈A的概率P2，并指出她与嘉嘉落回到圈A的可能性一样吗？

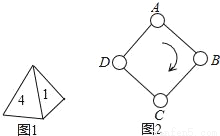
    （1）；（2）可能性一样． 【解析】试题分析：（1）根据概率公式求解即可；（2）列表求出所有等可能的结果，再求得淇淇随机掷两次骰子，最后落回到圈A的概率，比较即可解决. 试题解析： （1）掷一次骰子，有4种等可能结果，只有掷到4时，才会回到A圈. P1= (2)列表如下， 1 2 3 4 1 （1,1） （2,1） ...

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省兰州市中考数学模拟试卷 题型：单选题

    如图，点A、B、O是正方形网格上的三个格点，⊙O的半径为OA，点P是优弧AmB上的一点，则cos∠APB的值是（ ）

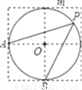
    A.45° B.1 C. 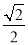D.无法确定

    C 【解析】由题意和正方形的性质得,∠AOB=90°， ∴∠APB=∠AOB=45°， ∴cos∠APB=. 故选：C.

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省兰州市中考数学模拟试卷 题型：单选题

    若反比例函数y=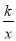的图象经过点（2，﹣6），则k的值为（　　）

    A. ﹣12 B. 12 C. ﹣3 D. 3

    A 【解析】试题分析：∵反比例函数的图象经过点（2，﹣6），∴，解得k=﹣12．故选A．

    查看答案和解析>>

    科目：初中数学 来源：山东省诸城市2018届九年级上学期期中联考数学试卷（Word版）. 题型：填空题

    计算=_____________．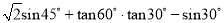

    【解析】试题分析：根据特殊角的三角函数值可得：sin45°=，tan60°=，tan30°=，sin30°=，原式=1+1-=．

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源九年一贯制学校中考数学模拟试卷 题型：解答题

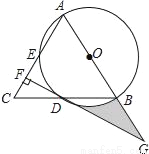
    如图，在△ABC中，AB=AC，以AB为直径的⊙O分别交线段BC，AC于点D，E，过点D作DF⊥AC，垂足为F，线段FD，AB的延长线相交于点G．

    （1）求证：DF是⊙O的切线；

    （2）若CF=2，DF=2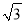，求图中阴影部分的面积．

    （1）证明见解析；（2）. 【解析】（1）连接AD、OD，由AB为直径可得出点D为BC的中点，由此得出OD为△BAC的中位线，再根据中位线的性质即可得出OD⊥DF，从而证出DF是⊙O的切线； （2）CF=1，DF=，通过解直角三角形得出CD=2、∠C=60°，从而得出△ABC为等边三角形，再利用分割图形求面积法即可得出阴影部分的面积． （1）证明：连接AD、OD，如图所示． ...

    查看答案和解析>>

    同步练习册答案