
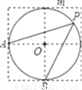
如图,点A、B、O是正方形网格上的三个格点,⊙O的半径为OA,点P是优弧AmB上的一点,则cos∠APB的值是( )
A.45° B.1 C. 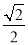 D.无法确定
D.无法确定
 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源:浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型:单选题
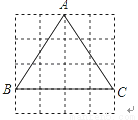
正方形网格中,△ABC如图放置,则sin∠BAC=( )
A. 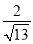 B.
B. 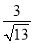 C.
C. 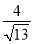 D.
D. 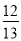
查看答案和解析>>
科目:初中数学 来源:湖南省邵阳县黄亭市2017~2018学年九年级数学(上)期末综合检测模拟题 题型:填空题
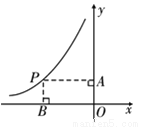
如图,点P是反比例函数y=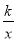 (x<0)图象上一点,PA垂直于y 轴,垂足为A,PB垂直于x轴,垂足为点B,若矩形 PBOA的面积为6,则k的值为_____.
(x<0)图象上一点,PA垂直于y 轴,垂足为A,PB垂直于x轴,垂足为点B,若矩形 PBOA的面积为6,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源:2017年甘肃省兰州市中考数学模拟试卷 题型:解答题
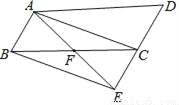
如图,延长平行四边形ABCD的边DC到点E,使CE=DC,连接AE,交BC于点F,连接AC、BE.
(1)求证:BF=CF;
(2)若AB=2,AD=4,且∠AFC=2∠D,求平行四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源:2017年甘肃省兰州市中考数学模拟试卷 题型:填空题
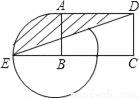
如图,已知矩形ABCD中,AD=2AB=2,以B为圆心,BA为半径作圆弧交CB的延长线于E,则图中阴影部分的面积是 .
查看答案和解析>>
科目:初中数学 来源:2017年甘肃省兰州市中考数学模拟试卷 题型:单选题
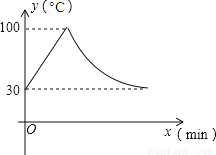
教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
A.7:20 B.7:30 C.7:45 D.7:50
A. 【解析】 试题分析:∵开机加热时每分钟上升10℃,∴从30℃到100℃需要7分钟. 设一次函数关系式为:y=k1x+b,将(0,30),(7,100)代入y=k1x+b得k1=10,b=30. ∴y=10x+30(0≤x≤7). 令y=50,解得x=2. 设反比例函数关系式为:,将(7,100)代入得k=700,∴。 将y=30代入,解得,∴(7≤x≤)....查看答案和解析>>
科目:初中数学 来源:2017年甘肃省兰州市中考数学模拟试卷 题型:单选题
一元二次方程x2+x+0.25=0的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 无实数根 D. 无法确定根的情况
B 【解析】a=1,b=1,c=0.25, b2-4ac=12-4×1×0.25=0, 所以方程有两个相等的实数根, 故选B.查看答案和解析>>
科目:初中数学 来源:山东省诸城市2018届九年级上学期期中联考数学试卷(Word版). 题型:单选题
如图,△ABC内接于⊙O,A为劣弧BC的中点,∠BAC=120°,过点B作⊙O的直径BD,连接AD,若AD=6,则AC的长为( )
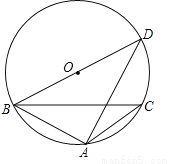
A. 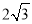 B.
B. 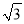 C. 2 D.
C. 2 D. 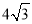
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源九年一贯制学校中考数学模拟试卷 题型:填空题
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列由5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1).其中正确的结论有_____.
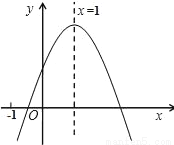
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com