练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    观察下列一组数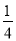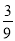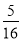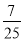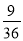： ， ， ， ， …，它们是按一定规律排列的，那么这一组数的第n个数是________．

    【解析】试题分析：观察已知一组数发现：分子为从1开始的连续奇数，分母为从2开始的连续正整数的平方，写出第n个数即可．根据题意得：这一组数的第n个数是. 故答案为：.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年湖北省随州市中考数学模拟试卷 题型：填空题

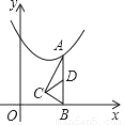
    如图,在平面直角坐标系中,点A在抛物线y=x2﹣2x+3上运动,过点A作AB⊥x轴于点B,以AB为斜边作Rt△ABC,则AB边上的中线CD的最小值为______．

    1. 【解析】试题分析：根据题意可知，当A点在抛物线的顶点（1，2）时，AB的长最短，最短为2，这时根据直角三角形斜边上的中线等于斜边的一半，可直接求解为CD=1. 故答案为：1.

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省黄冈市中考数学二模试卷 题型：解答题

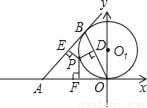
    如图，OB是以（O，a）为圆心，a为半径的⊙O1的弦，过B点作⊙O1的切线，P为劣弧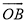上的任一点，且过P作OB、AB、OA的垂线，垂足分别是D、E、F．

    （1）求证：PD2=PE•PF；

    （2）当∠BOP=30°，P点为OB的中点时，求D、E、F、P四个点的坐标及S△DEF．

    （1）详见解析；（2）D（﹣a， a），E（﹣a， a），F（﹣a，0），P（﹣a， ）；S△DEF=a2． 【解析】试题分析：（1）连接PB，OP，利用AB切⊙O1于B求证△PBE∽△POD，得出，同理，△OPF∽△BPD，得出，然后利用等量代换即可． （2）连接O1B，O1P，得出△O1BP和△O1PO为等边三角形，根据直角三角形的性质即可解得D、E、F、P四个点的坐标．再利用三...

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省黄冈市中考数学二模试卷 题型：单选题

    二次函数y=ax2+bx+c的图象如下图所示，则一次函数y=bx+b2-4ac与反比例函数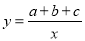在同一坐标系内的图象大致为（ ）

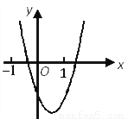
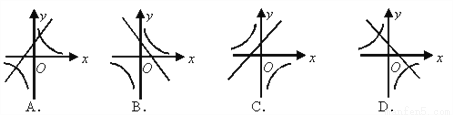
    A. （A） B. （B） C. （C） D. （D）

    D 【解析】观察二次函数图象可知开口方向向上，对称轴直线x＝－ ＞0，当x＝1时y＝a＋b＋c＜0，∴a>0，b<0，∴一次函数y＝bx＋a的图象经过第一、二、四象限，反比例函数y＝ 的图象在第二、四象限，只有D选项图象符合．故选D.

    查看答案和解析>>

    科目：初中数学 来源：吉林省吉林市2016-2017年七年级上期期末数学试卷 题型：解答题

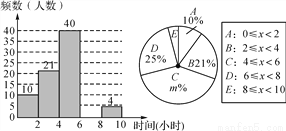
    某校想了解学生每周的课外阅读时间情况，随机调查了部分学生，对学生每周的课外阅读时间x(单位：小时)进行分组整理，并绘制了如图所示的不完整的频数直方图和扇形统计图：

    根据图中提供的信息，解答下列问题：

    (1)补全频数直方图；

    (2)求扇形统计图中m的值和E组对应的圆心角度数．

    （1）补图见解析；（2）14.4°. 【解析】试题分析： （1）由B组有21人和B组占抽查学生总数的21%可计算出被抽查学生的总数，由总数减去A、B、C、E各组的人数可得D组的人数，即可补全频数直方图； （2）由（1）中计算得到的总人数结合C组人数为40人，即可计算出C组占总数的百分比，从而得到：“m”的值；由E组人数4除以总人数再乘以360°即可得到扇形统计图中E组所对应的圆心...

    查看答案和解析>>

    科目：初中数学 来源：吉林省吉林市2016-2017年七年级上期期末数学试卷 题型：单选题

    某种商品每件的标价是330元，按标价的八折销售时，仍可获利10%，则这种商品每件的进价为( )

    A. 240元 B. 250元 C. 280元 D. 300元

    A 【解析】【解析】 设进价为x元，根据售价=进价×（1+利润率），列方程得：330×0.8=（1+10%）x 解得：x＝240，∴这种商品每件的进价为240元．故选A．

    查看答案和解析>>

    科目：初中数学 来源：吉林省吉林市2016-2017年七年级上期期末数学试卷 题型：单选题

    下面合并同类项正确的是( )

    A. 3x＋2x2＝5x3 B. 2a2b－a2b＝1 C. －ab－ab＝0 D. －xy2＋xy2＝0

    D 【解析】A.3x和2x2不是同类项不能合并，故A错； B.2a2b?a2b=a2b，故B错 C.?ab?ab=?2ab，故C错； D.?y2x+xy2=0，正确； 故选：D.

    查看答案和解析>>

    科目：初中数学 来源：吉林省长春市区2018届九年级上期末模拟数学试卷（解析版） 题型：填空题

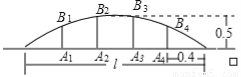
    某公园草坪的防护栏形状是抛物线形．为了牢固起见，每段护栏按0.4m的间距加装不锈钢的支柱，防护栏的最高点距底部0.5m（如图），则其中防护栏支柱A2B2的长度为 m．

    0.48. 【解析】 试题分析：根据所建坐标系特点可设解析式为y=ax2+c的形式，结合图象易求D点和C点坐标，代入解析式解方程组求出a，c的值得解析式；再根据对称性求出A2B2长度： 如图，建立平面直角坐标系，则由题意得D（0，0.5）、C（1，0）. 设抛物线的解析式为：y=ax2+c 代入得 a=-0.5，c=0.5，∴解析式为：. 当时y=0.48， ...

    查看答案和解析>>

    科目：初中数学 来源：福建省三明市大田县2018届九年级（上）期中数学试卷（解析版） 题型：解答题

    某超市在销售中发现：“宝宝乐”牌童装进价为60元，当定价为100元时，平均每天可售出20件，为了迎接“十一”国庆节，商场决定采取适当的降价措施，经调查发现：如果每件童装降价5元，那么平均每天就可多售出10件，要想平均每天盈利1200元，那么每件童装应该降价多少元？

    20元 【解析】试题分析：设每件童装降价元，那么平均每天就可多售出元，根据平均每天销售这种童装盈利1200元，即销量×每件的利润=1200元，列出方程求解即可． 试题解析：设每件童装应降价元，则 设每件童装应降价x元，则 (100?60?x)(20+2x)=1200， 即： 解得： ∵尽快减少库存， ∴舍去 答：每件童装应降价20元. ...

    查看答案和解析>>

    同步练习册答案