
��ͼ����BAD�͡�BCE��Ϊ����ֱ�������Σ���BAD=��BCE=90�㣬MΪDE���е�.����E����ADƽ�е�ֱ�ߣ�������AM�ڵ�N.
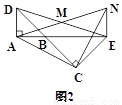
(1)��A��B��C������ͬһ��ֱ����ʱ(��ͼ1)����֤��MΪAN�е�.
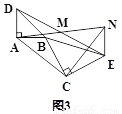
(2)��ͼ1�еġ�BCE�Ƶ�B��ת����A��B��E������ͬһ��ֱ����ʱ(��ͼ2)����֤����CANΪ����ֱ��������.
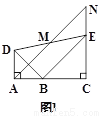
(3)��ͼ1�еġ�BCE�Ƶ�B��ת��ͼ3��λ��ʱ��(2)�еĽ����Ƿ���Ȼ����?����������֤����������������˵������.

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ�����������2017-2018ѧ�����ѧ�����п������꼶��ѧ�Ծ� ���ͣ������
���㣺
(1) 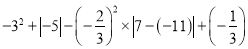
(2) 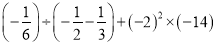
(3) 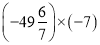
(4) 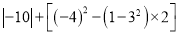
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�꽭��ʡ�����г����������Ծ���ѧ�Ծ� ���ͣ���ѡ��
���и�ʽ�У���ȷ���ǣ� ����
A. 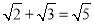 B.
B. 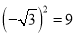 C.
C. 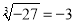 D.
D. 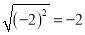
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����ɹ�2017���п���ѧ��ģ�Ծ� ���ͣ���ѡ��
��2017�����ɹų������п���ѧ��ģ����֪��sin(��x)=��sinx�� cos(��x)=cosx��sin��x+y��=sinxcosy+cosxsiny�������и�ʽ���������ǣ� ��
A. cos����45�㣩= 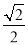 B. sin75��=
B. sin75��= 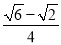
C. sin2x=2sinxcosx D. sin��x��y��=sinxcosy��cosxsiny
B ��������������Ŀ�����������㷽���ɵã�ѡ��A��cos����45�㣩=cos45��=��ѡ��B��sin75��=sin��30��+45�㣩=sin30��•cos45��+cos30��•sin45��=��+��=+��ѡ��C��sin2x=sinx•cosx+cosx•sinx=2sinx•cosx��ѡ��D��sin��x��y��=sinx•cos����y��+cosx•sin����y��=sinx•cosy��cosx•s...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����ɹ�2017���п���ѧ��ģ�Ծ� ���ͣ���ѡ��
��ͼ��AB��CD��AD��BC���ڵ�E������B=35�㣬��D=45�㣬���AEC=�� ��
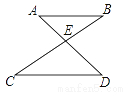
A. 35�� B. 45�� C. 70�� D. 80��
D ����������AB��CD����B=35�㣬 ���C=35�㣬 �ߡ�D=45�㣬 ���AEC=��C+��D=35��+45��=80�㣬 ��ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ɹ��п���ѧ��ģ�Ծ� ���ͣ������
��ͼ����֪����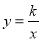 ��x��0����ͼ����A��B����B������Ϊ��2��2��������A��AC��x�ᣬ����ΪC������B��BD��y�ᣬ����ΪD��AC��BD���ڵ�F��һ�κ���y=ax+b��ͼ����A��D����x��ĸ����ύ�ڵ�E��
��x��0����ͼ����A��B����B������Ϊ��2��2��������A��AC��x�ᣬ����ΪC������B��BD��y�ᣬ����ΪD��AC��BD���ڵ�F��һ�κ���y=ax+b��ͼ����A��D����x��ĸ����ύ�ڵ�E��
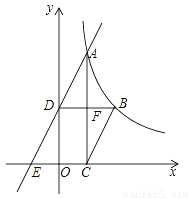
��1����AC=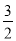 OD����a��b��ֵ��
OD����a��b��ֵ��
��2����BC��AE����BC�ij���
��1��a=��b=2����2��BC=�� �������������������1���������÷���������ͼ���ϵ���������ʵó�k��ֵ���ٵó�A��D�����꣬�������a��b��ֵ�� ��2����A�������Ϊ����m�� ������C�������Ϊ����m��0�����ó�tan��ADF=��tan��AEC=���������m��ֵ�����ɵó��𰸣� �����������1���ߵ�B��2��2���ں���y=��x��0����ͼ���ϣ� ��k=4����y=�� ��...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ɹ��п���ѧ��ģ�Ծ� ���ͣ������
�ֽ���ʽ��x3y��xy=�� ����
xy��x+1����x��1�� ��������ԭʽ=xy��x2��1��=xy��x+1����x��1���� �ʴ�Ϊ��xy��x+1����x��1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����ɹ�2018����꼶���ϣ�������ѧ�Ծ� ���ͣ������
�����з��̣���1��x2��12x��4=0�����䷽���� ��2��3��x��2��2=x��x��2��
��1��x1=6+2��x2=6��2����2��x1=2��x2=3�� ����������1������䷽�����������ɵó�����һԪһ�η��̣�������̵Ľ⼴�ɣ� ��2��������ٷֽ���ʽ�����ɵó�����һԪһ�η��̣�������̵Ľ⼴�� �������� ��1��x2��12x��4=0�� x2��12x=4�� x2��12x+36=4+36�� ��x��6��2=40�� x��6=�� x1=6+2��...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�γ��и�����2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
��ͼ����A��C��B�ڡ�O�ϣ���֪��AOB =��ACB = 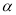 ����
����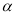 ��ֵΪ( )
��ֵΪ( )

A. 135�� B. 120�� C. 110�� D. 100��
B �����������ݡ�AOB=��ACB��˵���Ż�AB�Ķ������ӻ�AB�Ķ�����2�������ӻ�AB�Ķ���Ϊ120�ȣ����AOB=120��. ��ѡ��B.�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com