
课堂上,老师给出了一个只含字母x的多项式,并让同学们描述这个多项式的特征,以下是两位同学的描述,根据这些描述,请写出一个符合条件的多项式_____________.


科目:初中数学 来源:山东省潍坊市高密市2017-2018学年七年级(上)期中数学试卷 题型:填空题
小朋在用玩具枪瞄准时,总是用一只眼对准准星和目标,用数学知识解释为: .
两点确定一条直线 【解析】 试题分析:因为小朋在用玩具枪瞄准时,总是用一只眼对准准星和目标,这样它们在同一条直线上,所以用数学知识解释为:两点确定一条直线.查看答案和解析>>
科目:初中数学 来源:云南省2017-2018学年七年级上学期期中考试数学试卷 题型:填空题
商场内一款服装进价为a元,商家将其价格提高50%后以八折出售,则该款服装的售价是_________元.
1.2a 【解析】a×(1+50%)×0.8=1.2a. 故答案为1.2a.查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:解答题
已知:如图,△RPQ中,RP=RQ,M为PQ的中点.
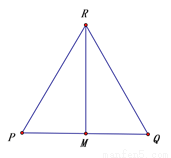
求证:RM平分∠PRQ.
证明:∵ M为PQ的中点(已知),
∴______=_______
在△______和△______中,

∴______≌______(_________).
∴ ∠PRM=______ (____________________________).
即RM平分∠PRQ.
PM QM RPM RQM QM RM RM △RQM ∠QRM 【解析】试题分析: 试题解析:证明:∵M为PQ的中点, ∴PM=QM. 在△PRM与△QRM中, ∵(已证), ∴△PRM≌△QRM(SSS), ∴∠PRM=∠QRM,即RM平分∠PRQ.查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:填空题
若分式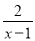 有意义,则x的取值范围是___________.
有意义,则x的取值范围是___________.
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:单选题
下列运算中正确的是( )
A. 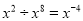 B.
B. 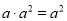 C.
C. 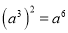 D.
D. 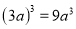
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期八年级数学期中试卷 题型:填空题
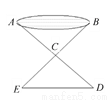
如图,有一池塘,要测池塘两端A、B两点的距离,可先在平地上取一个可以直接到达A、B两点的C,连接AC并延长AC到点D,使CD=CA,连结BC并延长BC到点E,使CE=CB,连接DE,那么量出________的长就等于AB的长. 这是因为可根据________方法判定△ABC≌△DEC.
查看答案和解析>>
科目:初中数学 来源:四川省江县初中2016年秋季七年级期末考试 题型:解答题
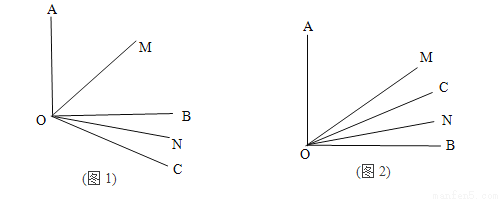
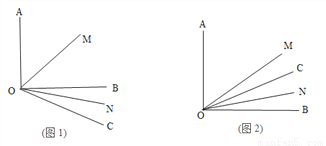
已知∠AOB=90°, 是锐角,ON平分
是锐角,ON平分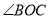 ,OM平分∠AOB.
,OM平分∠AOB.
(1)如图1若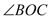 =30°,求
=30°,求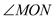 的度数?
的度数?
(2)若射线OC绕着点O运动到∠AOB的内部(如图2),在(1)的条件下求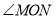 的度数;
的度数;
(3)若∠AOB=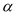 (90°≤
(90°≤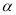 <180°),
<180°),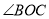 =
= 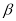 (0°<
(0°<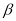 <90°),请用含有
<90°),请用含有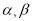 的式子直接表示上述两种情况
的式子直接表示上述两种情况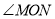 的度数.
的度数.
【答案】(1)60°;(2)30°;(3)①∠MON=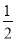 (
(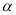 +
+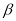 ),;②∠MON=
),;②∠MON=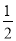 (
(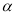 -
-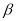 ).
).
【解析】试题分析:(1)由于∠AOB=90°,∠BOC=30°,OM平分∠AOB,ON平分∠BOC,所以可以求得∠MOB和∠NOB的度数,进而求得∠MON的度数;(2)类比(1)的方法求解即可;(3)结合(1)(2)题的计算方法求解即可.
试题解析:
(1)∵OM平分∠AOB,ON平分∠BOC,
∴∠BOM=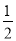 ∠AOB,∠BON=
∠AOB,∠BON=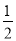 ∠BOC.
∠BOC.
∵∠AOB=90°,∠BOC=30°,
∴∠BOM=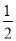 ×90°=45°,∠BON=
×90°=45°,∠BON=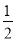 ×30°=15°,
×30°=15°,
∴∠MON=∠BOM+∠BON=45°+15°=60°.
(2)由(1)可知:∠BOM=45°,∠BON=15°,
∴∠MON=∠BOM-∠BON=45°-15°=30°.
(3)①∠MON=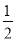 (
(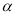 +
+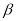 ),②∠MON=
),②∠MON=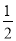 (
(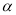 -
-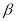 ).
).
点睛:本题主要考查学生角平分线的定义及角的计算的理解和掌握,在解决角与角之间的关系时,要充分利用已知条件和图中的隐含条件.
【题型】解答题
【结束】
27
(1)已知线段AB=8cm,在线段AB上有一点C,且BC=4cm,M为线段AC的中点.
①求线段AM的长?
②若点C在线段AB的延长线上,AM的长度又是多少呢?
(2)如图,AD=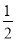 DB,E是BC的中点,BE=
DB,E是BC的中点,BE=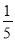 AC=2cm,求DE的长.
AC=2cm,求DE的长.
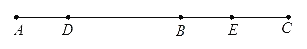
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com