
下列说法正确是
A. -2没有立方根 B. 8的立方根是±2
C. -27的立方根是-3 D. 立方根等于本身的数只有0和1
C 【解析】G根据立方根的性质,易得C.科目:初中数学 来源:2017年江苏省徐州市中考数学一模试卷 题型:填空题
函数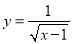 中,自变量x的取值范围是_____.
中,自变量x的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市2017-2018学年八年级上学期教学水平监测数学试卷 题型:解答题
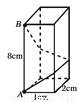
如图,长方体底面是长为2cm 宽为1cm的长方形,其高为8cm.
(1)如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,请利用侧面展开图计算所用细线最短需要多少?
(2)如果从点A开始经过4个侧面缠绕2圈到达点B,那么所用细线最短需要多少?
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市2017-2018学年八年级上学期教学水平监测数学试卷 题型:单选题
以下列各组数为边长,能构成直角三角形的是
A. 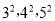 B. 6,8,10 C.
B. 6,8,10 C. 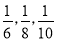 D.
D. 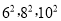
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市2017-2018学年八年级上学期教学水平监测数学试卷 题型:单选题
若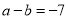 ,
, 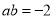 ,则
,则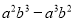 =( )
=( )
A. 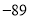 B.
B. 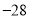 C. 89 D. 28
C. 89 D. 28
查看答案和解析>>
科目:初中数学 来源:2016-2017学年内蒙古呼伦贝尔市七年级(下)期中数学试卷 题型:解答题
解下列方程组
(1)(代入法)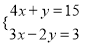
(2)(加减法)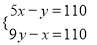 .
.
查看答案和解析>>
科目:初中数学 来源:2016-2017学年内蒙古呼伦贝尔市七年级(下)期中数学试卷 题型:填空题
如图,直线AB、CD相交于点O,OE⊥AB于点O,且∠COE=40°,则∠BOD为 .
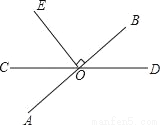
查看答案和解析>>
科目:初中数学 来源:2017-2018学年北师大版八年级数学下册 期中测评 题型:解答题
某办公用品销售商店推出两种优惠方法:①购1个书包,赠送1支水性笔;②购书包和水性笔一律按9折优惠.书包每个定价20元,水性笔每支定价5元.小丽和同学需买4个书包,水性笔若干支(不少于4支).
(1)分别写出两种优惠方法购买费用y(元)与所买水性笔支数x(支)之间的函数关系式;
(2)通过对x的取值情况进行分析,说明按哪种优惠方法购买比较便宜;
(3)小丽和同学需买这种书包4个和水性笔12支,请你设计怎样购买最经济.
(1) 见解析; (2)方案见解析;(3)最佳购买方案是:用优惠方法①购买4个书包,获赠4支水性笔;再用优惠方法②购买8支水性笔. 【解析】(1)设按优惠方法①购买需用y1元,按优惠方法②购买需用y2元, y1=(x-4)×5+20×4=5x+60, y2=(5x+20×4)×0.9=4.5x+72. (2)令y1>y2,即5x+60>4.5x+72,得x>24. 当...查看答案和解析>>
科目:初中数学 来源:四川省遂宁市2018届九年级上学期教学水平监测数学试卷 题型:单选题
化简: 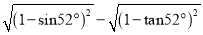 的结果是
的结果是
A. 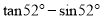 B.
B. 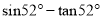
C. 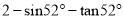 D.
D. 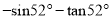
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com