
三角形一边长为10,另两边长是方程x2-14x+48=0的两根,则这是一个 三角形.
直角 【解析】【解析】 解方程得 ∵ ∴这个三角形为直角三角形 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 第3章 概率的进一步认识 单元测试卷 题型:填空题
做任意抛掷一只纸杯的重复试验,记录杯口朝上的次数,获得如下数据:
抛掷总次数 | 100 | 150 | 200 | 300 |
杯口朝上的频数 | 21 | 32 | 44 | 66 |
估计任意抛掷一只纸杯,杯口朝上的概率是________.
0.22 【解析】试题解析:∵21÷100=0.21; 32÷150≈0.21; 44÷200=0.22; 66÷300=0.22, ∴估计任意抛掷一只纸杯,杯口朝上的概率是0.22, 故答案为:0.22.查看答案和解析>>
科目:初中数学 来源:湖南邵阳市区2017-2018学年八年级上册数学期末试卷 题型:解答题
(8分)先化简,再求值:
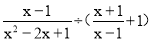 ,其中
,其中 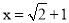
查看答案和解析>>
科目:初中数学 来源:湖南邵阳市区2017-2018学年八年级上册数学期末试卷 题型:单选题
下列命题是假命题的是( )
A. 三角形的角平分线都在三角形内部 B. 三角形的三条高都在三角形内部
C. 三角形的三条中线都在三角形内部 D. 三角形的三条角平分线相交于一点
B 【解析】A. ∵ 三角形的角平分线都在三角形内部是真命题,故不符合题意; B. ∵钝角三角形有两条条高在三角形外部,∴三角形的三条高都在三角形内部是假命题,故符合题意; C. ∵三角形的三条中线都在三角形内部是真命题,故不符合题意; D. ∵三角形的三条角平分线相交于一点是真命题,故不符合题意; 故选B.查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十七章达标检测卷 题型:解答题
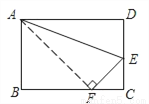
如图,折叠长方形的一边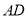 ,使点
,使点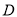 落在
落在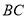 边上的点
边上的点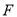 处,
处, 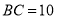 cm,
cm, 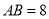 cm,求:
cm,求:
(1)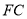 的长;
的长;
(2)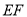 的长.
的长.
查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十七章达标检测卷 题型:单选题
三角形三边长分别是6,8,10,则它的最短边上的高为( )
A. 6 B. 14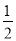 C. 2
C. 2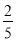 D. 8
D. 8
查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十七章达标检测卷 题型:单选题
直角三角形的一条直角边长是另一条直角边长的 ,斜边长为10,则它的面积为( )
,斜边长为10,则它的面积为( )
A. 10 B. 15 C. 20 D. 30
B 【解析】【解析】 直角三角形的一条直角边是另一条直角边的,设较短直角边是a,另一直角边是3a,根据勾股定理得:a2+(3a)2=100,解得:a=,则另一直角边是,则面积是:××=15.故选B.查看答案和解析>>
科目:初中数学 来源:湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型:单选题
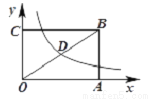
如图,矩形OABC的面积为24,它的对角线OB与双曲线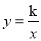 相交于点D,且D为OB的中点,则k的值为( )
相交于点D,且D为OB的中点,则k的值为( )
A. 3 B. 6 C. 9 D. 12
B 【解析】根据反比例函数解析式可得D点的坐标为(),然后根据中点的性质,可得B点的坐标为:(),然后可根据矩形的面积可求得2x×=24,解得k=6. 故选:B.查看答案和解析>>
科目:初中数学 来源:山西省吕梁市孝义市2016-2017学年九年级(上)期末考试数学试卷 题型:填空题
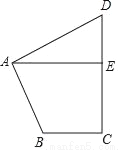
如图,在四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥CD,垂足为E,若线段AE=10,则S四边形ABCD=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com