练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，把斜边长为数学公式，一直角边长为1的两全等直角三角形纸片如图摆在桌面上，使直角重合，则两纸片覆盖桌面的面积是________．


    分析：根据勾股定理可得，AB=BD=2，则AE=BE=BC=CD=1，所以，S△AEF=S△BEF=S△BCF=S△CDF，即S△CDF=S△ABC，则两纸片覆盖桌面的面积=S△ABC+S△CDF，解答出即可．
    解答：解：∵AC=，BC=1，
    ∴AB=2，
    即AB=BD=2，BC=AE=BE=CD=1，
    ∵△ABC≌△DBE，
    ∴S△AEF=S△BEF=S△BCF=S△CDF，
    即S△CDF=S△AEF，
    又∵S△ABC=×1×2=1，
    ∴S△CDF=，
    ∴两纸片覆盖桌面的面积=S△ABC+S△CDF=1+=．
    故答案为：．
    点评：本题主要考查了直角三角形的性质和三角形的等积变换，掌握等底等高的两个三角形的面积相等．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

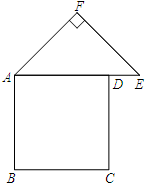    （2012•和平区一模）如图，有一张纸片，是由边长为a的正方形ABCD、斜边长为2b的等腰直角三角形FAE组成的（b＜a），∠AFE=90°，且边AD和AE在同一条直线上．要通过适当的剪拼，得到一个与之面积相等的正方形．
    （Ⅰ）该正方形的边长为
    		a2+b2
    		a2+b2
    ；
    （Ⅱ）现要求只能用两条裁剪线，请你设计一种裁剪的方法，在图中画出裁剪线，并简要
    说明剪拼的过程：
    ①在BA上截取BG=b；②画出两条裁剪线CGFG；③以点C为旋转中心，把△CBG顺时针旋转90°到△CDH的位置，以点F为旋转中心，把△FAG逆时针旋转90°到△FEH的位置．
    ①在BA上截取BG=b；②画出两条裁剪线CGFG；③以点C为旋转中心，把△CBG顺时针旋转90°到△CDH的位置，以点F为旋转中心，把△FAG逆时针旋转90°到△FEH的位置．
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，把斜边长为
    		5
    ，一直角边长为1的两全等直角三角形纸片如图摆在桌面上，使直角重合，则两纸片覆盖桌面的面积是
    4
    3
    4
    3
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：044

    如图①，直角三角形的两个锐角分别是40°和50°，其三边上分别有一个正方形．执行下面的操作：由两个小正方形向外分别作锐角为40°和50°的直角三角形，再分别以所得到的直角三角形的直角边为边长作正方形．图②是一次操作后的图形．

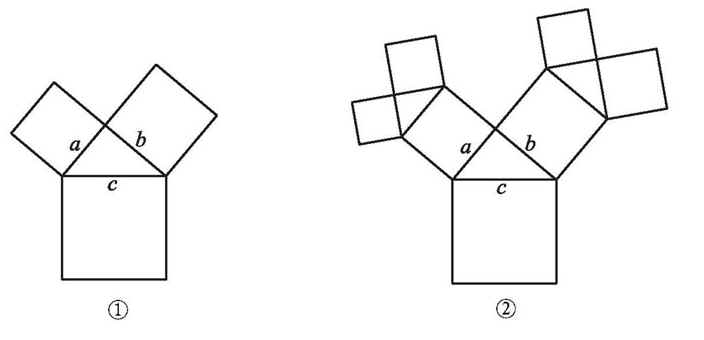
    (1)试画出2次操作后的图形．

    (2)如果原来直角三角形斜边长为1厘米，写出2次操作后的图形中所有正方形的面积和．

    (3)如果一直画下去，你能想像出它的样子吗？

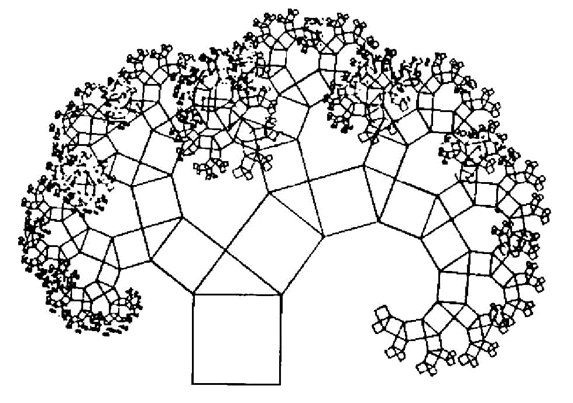
    (4)下图是重复上述步骤若干次后得到的图形，人们把它称为“毕达哥拉斯树”．如果最初的直角三角形等腰直角三角形，你能想像出此时“毕达哥拉斯树”的形状吗？

    　

    查看答案和解析>>

    科目：初中数学 来源：同步练习　　数学九年级下册 题型：044

    如图，把两个全等的等腰直角三角板ABC和EFG(其直角边长均为4)叠放在一起(如图①)，且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合，现将三角板EFG绕O点按顺时针方向旋转(旋转角α满足条件：＜α＜)，四边形CHGK是旋转过程中两三角板的重叠部分(如图②)．

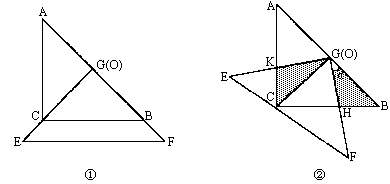
    (1)在上述旋转过程中，BH与CK有怎样的数量关系？四边形CHGK的面积有何变化？证明你发现的结论；

    (2)连接HK，在上述旋转过程中，设BH＝x，△GKH的面积为y，求y与x之间的函数关系式，并写出自变量x的取值范围；

    (3)在(2)的前提下，是否存在某一位置，使△GKH的面积恰好等于△ABC面积的？若存在求出此时x的值；若不存在，说明理由．

    查看答案和解析>>

    同步练习册答案