练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在△ABC中，D是BC边上一点，且AB=AD=DC，∠BAD=40°，则∠C为（　　）．

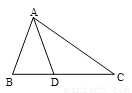
    A. 25° B. 35° C. 40° D. 50°

    B 【解析】因为AB=AD，所以°，又因为AD=DC，所以°。故选B
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2018人教版九年级数学下册练习：第二十六章 达标检测卷 题型：单选题

    若在同一直角坐标系中，正比例函数y＝k1x与反比例函数y＝的图象无交点，则有(　　)

    A. k1＋k2＞0 B. k1＋k2＜0 C. k1k2＞0 D. k1k2＜0

    D 【解析】当k1，k2同号时，正比例函数y＝k1x与反比例函数y＝的图象有交点；当k1，k2异号时，正比例函数y＝k1x与反比例函数y＝的图象无交点，即可得当k1k2＜0时，正比例函数y＝k1x与反比例函数y＝的图象无交点，故选D.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学北师大版上册：第2章 有理数及其运算 单元测试卷 题型：填空题

    在0，1，－2，－3.5这四个数中，是负整数的为________．

    －2 【解析】在0，1，－2，－3.5这四个数中，是负整数的为-2．

    查看答案和解析>>

    科目：初中数学 来源：四川省仁寿县2017-2018学年上学期八年级期末考试数学试卷 题型：解答题

    △ABC在平面直角坐标系中的位置如图所示．A（2，3），B（3，1），C（﹣2，﹣2）三点在格点上．

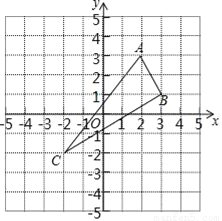
    （1）作出△ABC关于y轴对称的△A1B1C1；

    （2）直接写出△ABC关于x轴对称的△A2B2C2的各点坐标；

    （3）求出△ABC的面积．

    （1）作图见解析;（2）A2（2，﹣3），B2（3，﹣1），C2（﹣2，2）;（3）6.5． 【解析】试题分析：（1）先得到△ABC关于y轴对称的对应点，再顺次连接即可； （2）先得到△ABC关于x轴对称的对应点，再顺次连接，并且写出△ABC关于x轴对称的△A2B2C2的各点坐标即可； （3）利用轴对称图形的性质可得利用矩形的面积减去三个顶点上三角形的面积即可． 试题解析：...

    查看答案和解析>>

    科目：初中数学 来源：四川省仁寿县2017-2018学年上学期八年级期末考试数学试卷 题型：填空题

    已知一个多边形的内角和等于1260°，则这个多边形是______边形.

    9 【解析】设这个多边形的边数为，根据题意得： ， 解得： ，即该多边形是9边形. 故答案为：9.

    查看答案和解析>>

    科目：初中数学 来源：四川省仁寿县2017-2018学年上学期八年级期末考试数学试卷 题型：单选题

    若分式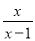有意义，则x的取值范围是（　　）

    A. x≠-1； B. x≠1； C. x≥-1； D. x≥1.

    B 【解析】∵分式有意义， ∴，解得： ，即的取值范围是： . 故选D.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册 第一章 整式的乘除 1.1 同底数幂的乘法 同步测试 含答案 题型：填空题

    计算：103×100×10＋2×10×105＝______(结果用幂的形式表示)．

    3×106 【解析】试题解析：103×100×10＋2×10×105 ＝103×102×10＋2×10×105 ＝106+2×106 =3×106 故答案为：3×106

    查看答案和解析>>

    科目：初中数学 来源：2018届中考数学一轮复习单元检测：第7讲 一元二次方程（组）及应用 题型：填空题

    在△ABC中BC=2，AB=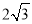，AC=b，且关于x的方程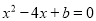有两个相等的实数根，则AC边上的中线长为______．

    2 【解析】∵关于x的方程x2-4x+b=0有两个相等的实数根， ∴△=16-4b=0， ∴AC=b=4， ∵BC=2，AB=2， ∴BC2+AB2=AC2， ∴△ABC是直角三角形，AC是斜边， ∴AC边上的中线长=AC==×4=2；

    查看答案和解析>>

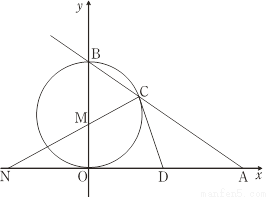
    科目：初中数学 来源：广东省汕头市龙湖区2018届九年级上学期期末质量检测数学试卷 题型：解答题

    如图，已知直线AB与x轴、y轴分别交于点A和点B，OA=4，且OA，OB长是关于x的方程x2﹣mx+12=0的两实根，以OB为直径的⊙M与AB交于C，连接CM，交x轴于点N，点D为OA的中点．

    （1）求证：CD是⊙M的切线； （2）求线段ON的长．

    （1）证明见解析；（2） NO=． 【解析】试题分析：（1）由OA、OB长是关于x的方程x2﹣mx+12=0的两实根，OA=4，则OA×OB=12，根据根与系数的关系可得OB=3，即可得⊙M的半径为1.5；因BM=CM=1.5，根据等腰三角形的性质可得∠OBA=∠BCM；连结OC，OB是⊙M的直径，则∠ACO=90°，D为OA的中点，根据直角三角形斜边的中线等于斜边的一半，可得OD=AD=C...

    查看答案和解析>>

    同步练习册答案