
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源:湖南省娄底市娄星区2017-2018学年九年级上学期期末考试数学试卷 题型:填空题
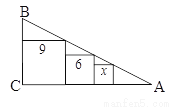
如图,在Rt△ABC内画有边长为9,6,x的三个正方形,则x的值为_________.
查看答案和解析>>
科目:初中数学 来源:上海市普陀区(五四制)2017-2018学年六年级上学期期末考试数学试卷 题型:填空题
16与20的最大公因数是__________.
4 【解析】16=2×2×2×2,20=2×2×5, 所以16和20的最大公因数是4, 故答案为:4.查看答案和解析>>
科目:初中数学 来源:贵州省黔南州2017-2018学年八年级上学期期末联考数学试卷 题型:填空题
PM 2.5是指大气中直径小于或等于0.0000025m的颗粒物,将0.0000025用科学记数法表示为________.
2.5×10﹣6 【解析】试题分析:绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定. 试题解析:0.0000025=2.5×10-6.查看答案和解析>>
科目:初中数学 来源:贵州省黔南州2017-2018学年八年级上学期期末联考数学试卷 题型:单选题
下列计算正确的是( )
A.  B.
B. 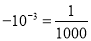 C.
C. 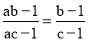 D.
D. 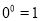
查看答案和解析>>
科目:初中数学 来源:山东省青岛市2017-2018学年上学期期末考试八年级数学试卷 题型:解答题
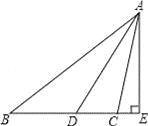
如图,∠ABC=38°,∠ACB=100°,AD平分∠BAC,AE是BC边上的高,求∠DAE的度数.
查看答案和解析>>
科目:初中数学 来源:山东省青岛市2017-2018学年上学期期末考试八年级数学试卷 题型:单选题
如图,在△ABC中,∠C=90°,∠ABC=60°,BD平分∠ABC,若AD=8,则CD等于( )

A. 3 B. 4 C. 5 D. 6
B 【解析】∵∠ACB=90°,∠ABC=60°, ∴∠A=30°, ∵BD平分∠ABC, ∴∠CBD=∠DBA=30°, ∴BD=AD, ∵AD=8, ∴BD=8, ∴CD=BD=4. 故选:B.查看答案和解析>>
科目:初中数学 来源:新疆乌鲁木齐市2018届九年级上学期期末考试数学试卷 题型:解答题
某地区2015年投入教育经费2500万元,2017年投入教育经费3025万元
(1)求2015年至2017年该地区投入教育经费的年平均增长率;
(2)根据(1)所得的年平均增长率,预计2018年该地区将投入教育经费多少万元?
(1)10%.(2)3327.5万元. 【解析】试题分析:(1)、设增长率为x,然后根据一般公式:增长前的数量×(1+增长率)增长次数=增长后的数量列出一元二次方程,从而得出答案;(2)、根据增长率求出2018年的教育经费. 试题解析:(1)、【解析】 设增长率为x,根据题意2016年为2500(1+x)万元, 2017年为2500(1+x)2万元.则2500(1+x)2=30...查看答案和解析>>
科目:初中数学 来源:江苏省盐城市盐都区2017届九年级上学期期末考试数学试卷 题型:解答题
某公司在销售一种产品进价为10元的产品时,每年总支出为10万元(不含进货支出).经过若干年销售得知,年销售量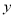 (万件)是销售单价
(万件)是销售单价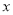 (元)的一次函数,并得到如下部分数据:
(元)的一次函数,并得到如下部分数据:
销售单价 | 12 | 14 | 16 | 18 |
年销售量 | 7 | 6 | 5 | 4 |
(1)求出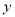 关于
关于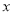 的函数关系式;
的函数关系式;
(2)写出该公司销售这种产品的年利润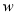 (万元)关于销售单价
(万元)关于销售单价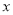 (元)的函数关系式;当销售单价
(元)的函数关系式;当销售单价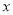 为何值时,年利润最大?
为何值时,年利润最大?
(3)试通过(2)中的函数关系式及其大致图象,帮助该公司确定产品的销售单价范围,使年利润不低于20万元(请直接写出销售单价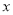 的范围).
的范围).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com