
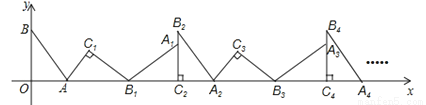
如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△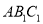 的位置,点B,O分别落在点
的位置,点B,O分别落在点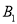 ,
,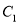 处,点
处,点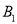 在
在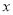 轴上,再将△
轴上,再将△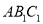 绕点
绕点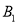 顺时针旋转到△
顺时针旋转到△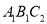 的位置,点
的位置,点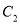 在
在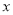 轴上,将△
轴上,将△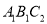 绕点
绕点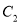 顺时针旋转△
顺时针旋转△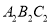 的位置,点
的位置,点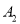 在
在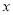 轴上……依次进行下去。若点
轴上……依次进行下去。若点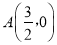 ,B(0,2),则点
,B(0,2),则点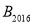 的坐标为_____________ .
的坐标为_____________ .
 习题精选系列答案
习题精选系列答案科目:初中数学 来源:上海市崇明区2018届九年级上学期期末调研测试数学试卷 题型:填空题
如果一幅地图的比例尺为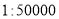 ,那么实际距离是
,那么实际距离是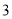 km的两地在地图上的图距是_________cm.
km的两地在地图上的图距是_________cm.
查看答案和解析>>
科目:初中数学 来源:河南省商丘市2017-2018学年上期九年级数学期末第一次模拟试卷 题型:解答题
如图,已知AB∥CD,AD,BC相交于E,F为EC上一点,且∠EAF=∠C.
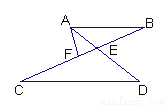
求证:(1) ∠EAF=∠B; (2)AF2=FE·FB
证明见解析 【解析】(1)∵AB∥CD,∴∠B=∠C (2分) 又∵∠EAF=∠C,∴∠EAF=∠B (4分) (2)在⊿AFB与⊿EFA中,∵∠EAF=∠B,∠AFB=∠EFA,∴⊿AFB=∽⊿EFA (6分) ∴,即AF2=FE·FB (8分) (1)欲证∠EAF=∠B,通过AB∥CD及已知发现它们都与∠C相等,等量转换即可; (2)欲证AF2=FE•FB,可证△...查看答案和解析>>
科目:初中数学 来源:河南省商丘市2017-2018学年上期九年级数学期末第一次模拟试卷 题型:单选题
(2016河北省)如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
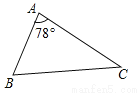
A. 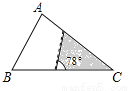 B.
B. 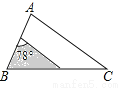
C. 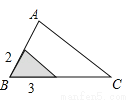 D.
D. 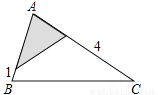
查看答案和解析>>
科目:初中数学 来源:广东省江门市江海区五校2018届九年级上学期期末联考数学试卷 题型:解答题
不透明的口袋里装有白、黄、蓝三种颜色的乒乓球(除颜色外其余都相同),其中白球有2个,黄球有1个,再从中任意摸出1个球是白球的概率为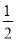 .
.
(1)试求袋中蓝球的个数;
(2)第一次任意摸出一个球(不放回),第二次再摸出一个球,请用树状图或列表法表示两次摸到球的所有可能结果,并求两次摸到的球都是白球的概率.
(1)蓝球有1个;(2) 【解析】试题分析:(1)先根据白球的概率是,可求出球的总数,然后用求得的球的总个数减去白球和黄球的个数即可; (2)画出树状图可知,共有12种可能结果,两次摸到的球都为白球的情况有2种,从而可求出两次摸到的球都是白球的概率. 【解析】 (1)总球数为个,4-2-1=1 ∴蓝球有1个 (2) 开始 第一次 白1 白2 黄 蓝 第二...查看答案和解析>>
科目:初中数学 来源:广东省江门市江海区五校2018届九年级上学期期末联考数学试卷 题型:填空题
平面直角坐标系内,与点P(-1, 3)关于原点对称的点的坐标为____________.
(1,-3) 【解析】平面直角坐标系内,与点P(-1, 3)关于原点对称的点的坐标为(1,-3.查看答案和解析>>
科目:初中数学 来源:广东省江门市江海区五校2018届九年级上学期期末联考数学试卷 题型:单选题
小玲在一次班会中参与知识抢答活动,现有语文题6个,数学题5个,英语题9个,她从中随机抽取1个,抽中数学题的概率是( )
A. 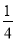 B.
B. 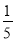 C.
C. 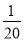 D.
D. 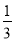
查看答案和解析>>
科目:初中数学 来源:山东省淄博市2017-2018学年七年级上学期期中考试数学试卷 题型:单选题
若m,n互为相反数,c,d互为倒数,则代数式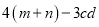 的值为( ) .
的值为( ) .
A. 4 B. -1 C. -3 D. 0
C 【解析】∵m、n互为相反数,∴m+n=0, ∵c、d互为倒数,∴cd=1, 则代数式4(m+n)?3cd=4×0?3×1=?3. 故选:C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年陕西安市九年级(上)期末数学试卷 题型:解答题
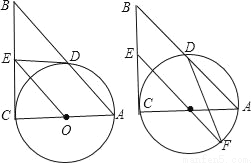
如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)如果⊙O的半径为 ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com