
ij��ѧΪ�˱������鷨�����гɼ�ͻ����ѧ���������˸ֱ�30֧��ë��45֧��������1755Ԫ������ÿ֧ë�ʱȸֱʹ�4Ԫ��
��1����ֱʺ�ë�ʵĵ��۸�Ϊ����Ԫ��
��2����ѧУ����Ҫ������������ֱʹ�105֧��ÿ�ֱʵĵ��۲��䣩������ʦ����Ԥ������������ʦ˵����������������ֱ���֧��2447Ԫ��������ʦ����һ�£�˵�������������ЩǮֻ�������ֱʣ���ô�ʿ϶�����ˣ���������ѧ���ķ���֪ʶ��������ʦΪʲô˵������ЩǮֻ�������ֱʵ�������ˣ�
�ڳ���ʦͻȻ����������Ԥ���л�����У���������һ֧ǩ�ֱʣ����ǩ�ֱʵĵ���ΪС��10Ԫ����������ͨ�����㣬ֱ��д��ǩ�ֱʵĵ��ۿ���Ϊ Ԫ��
��1���ֱʵĵ���Ϊ21Ԫ��ë�ʵĵ���Ϊ25Ԫ����2���ٽ��ͼ���������2Ԫ��6Ԫ�� �������� �����������1����ֱʵĵ���ΪxԪ����ë�ʵĵ���Ϊ��x+4��Ԫ��������ֱ�30֧��ë��45֧��������1755Ԫ�������̣������⼴�ɣ� ��2���ٸ��ݵ�һ�ʵĽ����赥��Ϊ21Ԫ�ĸֱ�Ϊy֧�����Ե���Ϊ25Ԫ��ë����Ϊ��105��y��֧��������̵Ľⲻ��������˵������ˣ� ���赥��Ϊ21Ԫ...
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ�����������2016-2017ѧ�����ѧ����ĩ���Ծ��꼶��ѧ�Ծ� ���ͣ������
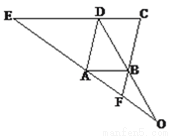
��ͼ,��֪EC��AB,��EDA=��ABF.
(1)��֤���ı���ABCD��ƽ���ı��Σ�
(2)ͼ�д��ڼ������������Σ��ֱ���ʲô����ֱ��д��������֤����
(3)��֤��OA2=OE?OF.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡΫ���������2016-2017ѧ����꼶���ϣ���ĩ��ѧ�Ծ� ���ͣ���ѡ��
��ͼ��ʾ��������������������AC=AB����AB��CD���ۡ�1=��2������������������ѡ������Ϊ���裬��һ����Ϊ���ۣ������������ĸ���Ϊ��������
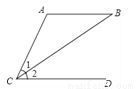
A. 0 B. 1 C. 2 D. 3
D �����������еȿ��ܵ������3�֣��ֱ�Ϊ�٢�⇒�ۣ��٢�⇒�ڣ��ڢ�⇒�٣�������������������������У��٢�⇒�ۣ��٢�⇒�ڣ��ڢ�⇒�٣� ��ѡ��D.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�Ϸ���2016~17ѧ��ȵ�һѧ�� ��ĩ��ѧ������� ���꼶��ѧ�Ծ� ���ͣ������
��ͼ��ʾ������AΪ120��ĵ�����ABC�У�DE��ֱƽ��AB��D����DE��2����EC��_________��
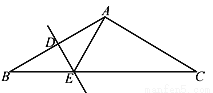
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�Ϸ���2016~17ѧ��ȵ�һѧ�� ��ĩ��ѧ������� ���꼶��ѧ�Ծ� ���ͣ���ѡ��
��ͼ���ڡ�ABC�У���BAC��90�㣬AB��3��AC��4��BC��5��EF��ֱƽ��BC����PΪֱ��EF�ϵ���һ�㣬��AP��BP����Сֵ�ǣ�������
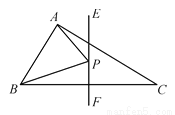
A. 3 B. 4 C. 5 D. 6
B �������������������������֪��B����ֱ��EF�ĶԳƵ�Ϊ��C���ʵ���P���D�غ�ʱ��AP+BP����Сֵ�����AC���ȼ��ɣ� �������� ��EF��ֱƽ��BC�� ��B��C����EF�Գƣ� AC��EF��D�� �൱P��D�غ�ʱ��AP+BP��ֵ��С����Сֵ����AC�ij��� �ɹ��ɶ����ã�AC==4�� �ʴ�Ϊ��4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ������꼶��ѧ�ϲ���ĩ���Ծ� ���ͣ������
�Ȼ�������ֵ�� 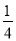 ����4x2+2x��8������
����4x2+2x��8������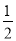 x��1��������x=
x��1��������x=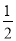 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ������꼶��ѧ�ϲ���ĩ���Ծ� ���ͣ������
���㣺15��37��+42��51��=_________��
58��28�� �������������������ֱ�ӽ��ȷ�����Ӧλ���ϵ�����ӣ��ٰ���60��һ��ԭ����ǰ��λ���ɣ� ���������15��37��+42��51��=57��88��=58��28�䣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����ɹ������첼�з�У���꼶���ϣ�������ѧ�Ծ� ���ͣ������
ABCD�У�E��CD����һ�㣬
��1������ADE�Ƶ�A��˳ʱ�뷽����ת��ʹAD��AB�غϣ��õ���ABF����ͼ1��ʾ���۲��֪����DE��ȵ��߶����� ������AFB=���� ��
��2����ͼ2��������ABCD�У�P��Q�ֱ���BC��CD���ϵĵ㣬�ҡ�PAQ=45�㣬��ͨ����ת�ķ�ʽ˵����DQ+BP=PQ��
��3���ڣ�2�����У�����BD�ֱ�AP��AQ��M��N���㻹������ת��˼��˵��BM2+DN2=MN2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶���ϣ�������ѧ�Ծ� ���ͣ������
���x2-2��m+1��x+4��һ����ȫƽ����ʽ����m= ��
-3��1 �������� �����������x2-2��m+1��x+4��һ����ȫƽ����ʽ�� ��-2��m+1��=��4�� ��m=-3��1���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com