
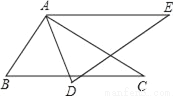
��ͼ����ABC�ա�ADE����AB=_____����E=��_____������BAE=120�㣬��BAD=40�㣬���BAC=_____��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��������Դ��2016-2017ѧ���һѧ����ĩ�������꼶��ѧ�Ծ� ���ͣ���ѡ��
��a + b = 6����18��2a��2b =�� ��
A. 6 B. ��6 C. ��24 D. 12
A ��������18��2a��2b =18-2(a+b)=18-2=6.��ѡA.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ��ӱ�ʡ�żҿ����Ŷ������꼶���£���ĩ��ѧ�Ծ� ���ͣ���ѡ��
��ͼ����ABC�С�A=30�㣬E��AC���ϵĵ㣬�Ƚ���ABE����BE���ۣ����ۺ��ABE��AB�߽�AC�ڵ�D���ֽ���BCD����BD���ۣ�C��ǡ������BE�ϣ���ʱ��CDB=82�㣬��ԭ�����εġ�B=���������ȣ�
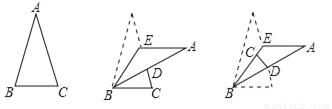
A. 78�� B. 52�� C. 68�� D. 75��
A ���������ڡ�ABC�У���A=30�㣬���B+��C=150��٣� �����۵�������֪����B=3��CBD����BCD=��C�� �ڡ�CBD�У����У���CBD+��BCD=180�㩁82�㣬���� ��B+��C=98��ڣ� �٩��ڣ��ã� ��B=52�㣬 ��á�B=78�㣬 ��ѡA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ������
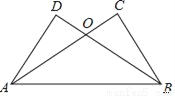
��ͼ����֪AC��BC��BD��AD��AC��BD����O��AC=BD��
��֤����1��BC=AD��
��2����OAB�ǵ��������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ������
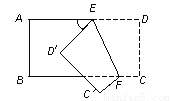
��ͼ����һ��������ֽƬ��EF�۵���D��C�ֱ�����D�䣬C���λ�ã�����EFB��65�㣬���AED��Ķ���Ϊ_________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
��ͼ����֪��ABCΪֱ�������Σ���C=90�㣬����ͼ������ȥ��C�����1+��2=��������
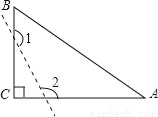
A. 90�� B. 135�� C. 270�� D. 315��
C ���������������:�ȸ���ֱ�������ε��������������Ǻ���90�ȣ��ٸ����ı��ε��ڽǺ���360�ȣ�������á�1+��2��ֵ�� �������� �ߡ�C=90�㣬 ���A+��B=90�㣮 �ߡ�A+��B+��1+��2=360�㣬 ���1+��2=360�㩁90��=270�㣮 ��ѡ��C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�Ƹ���2017-2018ѧ����꼶���ϣ�������ѧ�� ���ͣ������
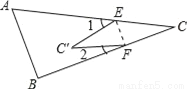
��ͼ������ABC�۵���ʹ��C���ڵ�C�䴦���ۺ�ΪEF��
��1������1=40�㣬��2=20�㣬���C��
��2��̽����1����2���C֮���������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�Ƹ���2017-2018ѧ����꼶���ϣ�������ѧ�� ���ͣ���ѡ��
��ͼ��DΪ��ABC��ƽ������һ�㣬PΪƽ����������D��һ�㣬PA��BA��PC��BC������ֱ�ΪA��C�������н��۴�����ǣ�������
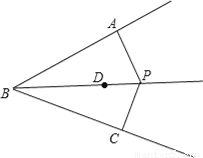
A. AD=CD B. ��DAP=��DCP C. ��ADB=��BDC D. PD=BD
D ������������������ߵ�D�ǡ�ABC��ƽ������һ�㣬��P��BD�ϣ�PA��AB��PC��BC�� ��գ� ���ڡ�APD�͡�CPD�У� ��գ� ����������һ���벻ͬ�ĵ㣬 ��һ�������� ��ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ�����꼶��ѧ�ڵڶ����¿���ѧ�Ծ� ���ͣ������
�Ȼ�������ֵ����3��x2��2x��+2��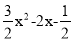 ��������x=4
��������x=4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com