
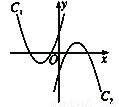
如图所示,已知抛物线C1,抛物线C2关于原点中心对称.如果抛物线C1的解析式为y= (x+2)2-1,那么抛物线C2的解析式为____________________.
(x+2)2-1,那么抛物线C2的解析式为____________________.
科目:初中数学 来源:甘肃省平凉市2017-2018学年八年级(上)期中数学试卷 题型:填空题
一个凸多边形的内角和是外角和的7倍,它是______边形.
十六. 【解析】设多边形边数为n,根据多边形的内角和公式可得360°×7=(n﹣2)•180°,解得n=16.查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学人教版上册:第3章 一元一次方程 单元测试卷 题型:解答题
(8分)已知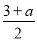 与
与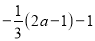 互为相反数,求a的值.
互为相反数,求a的值.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学人教版上册:第3章 一元一次方程 单元测试卷 题型:单选题
长沙红星大市场某种高端品牌的家用电器,若按标价打八折销售该电器一件,则可获纯利润500元,其利润率为20%.现如果按同一标价打九折销售该电器一件,那么获得的纯利润为( )
A. 562.5元 B. 875元 C. 550元 D. 750元
B 【解析】试题分析:利润率=(售价-进价)÷进价×100%,标价=售价÷折扣. 进价:500÷20%=2500元 售价:(2500+500)÷80%=3750元 3750×90%-2500=875元.查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学人教版上册:第23章 旋转 单元测试卷 题型:解答题
请你画出一条直线,把如图所示的平行四边形和圆两个图形分成面积相等的两部分(保留作图痕迹).

查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学人教版上册:第23章 旋转 单元测试卷 题型:填空题
请写出一个是中心对称图形的几何图形的名称: .
平行四边形(答案不唯一)。 【解析】【解析】 平行四边形是中心对称图形. 故答案可为:平行四边形.查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学人教版上册:第23章 旋转 单元测试卷 题型:单选题
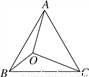
如图,O是等边△ABC内的一点,OB=1,OA=2,∠AOB=150°,则OC的长为( )
A. 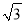 B.
B. 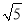 C.
C. 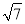 D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学人教版上册:第25章 概率初步 单元测试卷 题型:填空题
如图,一个转盘被分成7个相同的扇形,颜色分为红、黄、绿三种,指针的位置固定,转动转盘后任其自由停止,其中时某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),则指针指向红色的概率为___________.
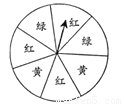
查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:第二十七章 达标检测卷 题型:解答题
如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.
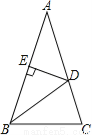
(1)写出图中一对全等三角形和一对相似比不为1的相似三角形;
(2)选择(1)中一对加以证明.
(1)△ADE≌△BDE,△ABC∽△BCD;(2)证明见解析. 【解析】试题分析:(1)利用相似三角形的性质以及全等三角形的性质得出符合题意的答案; (2)利用相似三角形的判定以及全等三角形的判定方法分别得出即可. 试题解析:【解析】 (1)△ADE≌△BDE,△ABC∽△BCD; (2)证明:∵AB=AC,∠A=36°, ∴∠ABC=∠C=72°, ∵BD...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com