
已知b<0,关于x的一元二次方程(x-1)2=b的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 没有实数根 D. 有两个实数根
C 【解析】试题分析:∵(x﹣1)2≥0,而b<0, ∴(x﹣1)2=b没有实数根. 故选C.科目:初中数学 来源:人教版九年级上册数学 第24章小结与复习 练习 题型:填空题
如图,AB切⊙O于点B,OA=2,∠OAB=30°,弦BC∥OA,劣弧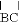 的弧长为 .(结果保留π)
的弧长为 .(结果保留π)
查看答案和解析>>
科目:初中数学 来源:《概率的进一步认识》单元测试2 题型:填空题
从装有5个红球和3个白球的袋中任意取4个,那么取到的“至少有1个是红球”与“没有红球”的概率分别为 和 。
1,0 【解析】 试题分析:根据必然事件和不可能事件的概率即可作出判断. 由题意得取到的“至少有1个是红球” 的概率为1,取到的“没有红球”的概率为0.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 21.2.1配方法(1)练习 题型:解答题
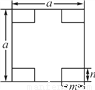
如图,在边长为a的正方形纸片的四个角都剪去一个长为m,宽为n的矩形.
(1)用含a,m,n的式子表示纸片剩余部分的面积;
(2)当m=3,n=5,且剩余部分的面积等于229时,求正方形的边长a的值.
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 21.2.1配方法(1)练习 题型:单选题
给出一种运算:对于函数y=xn,规定y′=nxn-1.例如:若函数y=x4,则有y′=4x3.已知函数y=x3,则方程y′=12的解是( )
A. x1=4,x2=-4 B. x1=2,x2=-2 C. x1=x2=0 D. x1=2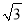 ,x2=-2
,x2=-2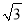
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 21.2.1配方法(1)练习 题型:填空题
若代数式3x2+1的值等于28,则x的值为___________.
3或-3 【解析】根据题意得3x2+1=28,即3x2=27,所以x=3或-3. 故答案为3或-3.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 23.3课题学习图案设计 测试 题型:填空题
基本图案在轴对称、平移、旋转变化的过程中,图形的______和______都保持不变.
形状, 大小. 【解析】轴对称、平移、旋转变化都是全等变化,所以在变化的过程中,图形的形状和大小不变,只是位置在变化. 故答案为(1)形状;(2)大小.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 23.1图形的旋转(2)测试 题型:单选题
如图,摆放有五杂梅花,下列说法错误的是(以中心梅花为初始位置)( )
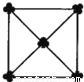
A. 左上角的梅花只需沿对角线平移即可
B. 右上角的梅花需先沿对角线平移后,再顺时针旋转45°
C. 右下角的梅花需先沿对角线平移后,再顺时针旋转180
D. 左下角的梅花需先沿对角线平移后,再顺时针旋转90°
B 【解析】由平移和旋转可得,D选项中左下角的梅花需要先沿着对角线平移后,再逆时针旋转90°,所以B选项错误,故选B.查看答案和解析>>
科目:初中数学 来源:《概率的进一步认识》单元测试4 题型:单选题
某市民政部门:“五一”期间举行“即开式福利彩票”的销售活动,发行彩票10万张(每张彩票2元),在这此彩票中,设置如下奖项:
奖金(元) | 1000 | 500 | 100 | 50 | 10 | 2 |
数量(个) | 10 | 40 | 150 | 400 | 1000 | 10000 |
如果花2元钱购买1张彩票,那么所得奖金不少于50元的概率是( )
A. 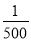 B.
B. 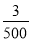 C.
C. 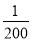 D.
D. 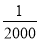
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com