练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    在一次函数y=（2m+2）x+4中，y随x的增大而增大，那么m的值是（ ）

    A.0 B.-1 C.-1.5 D.-2

    A. 【解析】 试题分析：当2m+2＞0时，一次函数y=2m+2x+1的值随x的增大而增大， 即m＞-1， 所以m可取0． 故选A.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：浙江杭州西湖区保俶塔实验学校2017-2018学年八年级上学期期中数学试卷 题型：填空题

    已知三角形三边长分别是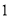、、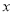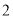，且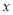为整数，那么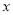的值是__________．

    2 【解析】根据三角形三边关系， ， ∵为整数， ∴， 故答案为：2.

    查看答案和解析>>

    科目：初中数学 来源：河南省周口市西华县2017-2018学年七年级上学期期末考试数学试卷 题型：解答题

    计算：（1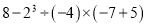）；（2）．

    （1）4；（2）20 【解析】试题分析：根据有理数混合运算法则计算即可． 试题解析：【解析】 （1）原式=8﹣8÷（﹣4）×（﹣2）=8﹣（﹣2）×（﹣2）= 8﹣4= 4； （2）原式= == 20．

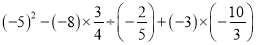    查看答案和解析>>

    科目：初中数学 来源：山东省枣庄市2017-2018学年八年级（上）期中数学复习试卷 题型：解答题

    某电信公司手机有两类收费标准，A类收费标准如下：不管通话时间多长，少，每部手机每月必须缴月租费12元，另外，通话费按0.2元/min计。B类收费标准如下：没有月租费，但通话费按0.25元/min计。

    (1)分别写出A、B两类每月应缴费用y（元）与通话时间x（min）之间的关系式；

    (2)如果手机用户预算每月交55元的话费，那么该用户选择哪类收费方式合算？

    (3)每月通话多长时间，按A、B两类收费标准缴费，所缴话费相等？

    (1)A类： ,B类： ；（2）；（3）240分钟 【解析】试题分析：（1）根据题目中收费标准可列出函数关系式； （2）分别由A、B两类收费关系式可求得相应的通话时间，时间久则更合算； （3）令两函数关系式相等可求得x的值，可求得答案． 试题解析： （1）A类：y=0.2x+12，B类：y=0.25x； （2）当y=55时， A类通话时间：55=0.2x+12，解得x=2...

    查看答案和解析>>

    科目：初中数学 来源：山东省枣庄市2017-2018学年八年级（上）期中数学复习试卷 题型：填空题

    如图，象棋盘上，若“将”位于点（0，-2），“车”位于点（-4，-2），则“马”位于点___________．

    （3，1） 【解析】观察棋盘，根据“将”位于点（0，-2），“车”位于点（-4，-2），可知“马”位于点（3，1），故答案为：（3，1）.

    查看答案和解析>>

    科目：初中数学 来源：山东省枣庄市2017-2018学年八年级（上）期中数学复习试卷 题型：单选题

    点A在直角坐标系中的坐标是(3,?4),则点A到y轴的距离是( )

    A. 3 B. ?4 C. 4 D. -3

    A 【解析】点A (3，?4)到y轴的距离是3，故选 A.

    查看答案和解析>>

    科目：初中数学 来源：山东省枣庄市2017-2018学年八年级（上）期中数学复习试卷 题型：单选题

    一架25分米长的梯子，斜立在一竖直的墙上，这时梯足距离墙底端7分米.如果梯子的顶端沿墙下滑4分米，那么梯足将滑动(　 )

    　

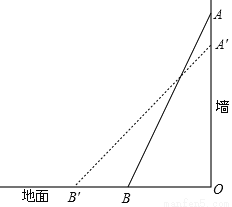
    A. 9分米 B. 15分米 C. 5分米 D. 8分米

    D 【解析】如下图所示： AB相当于梯子，△ABO是梯子和墙面、地面形成的直角三角形，△OCD是下滑后的形状，∠O=90°， 即：AB=CD=25分米，OB=7分米，AC=4分米，BD是梯脚移动的距离。 在Rt△ACB中，由勾股定理可得： AB2=AC2+BC2， AC= =24分米， ∴OC=AC?AC=24?4=2分米， 在Rt△COD中，由勾股...

    查看答案和解析>>

    科目：初中数学 来源：贵州省2017-2018学年八年级（上）期中数学试卷 题型：填空题

    小明从平面镜中看到镜子对面电子钟示数如图所示，这时的时刻应是 ．

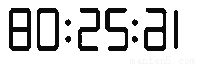
    16∶25∶08 【解析】【解析】 ∵是从镜子中看， ∴对称轴为竖直方向的直线， ∵5的对称数字为2，2的对称数字是5，镜子中数字的顺序与实际数字顺序相反， ∴这时的时刻应是16：25：08．

    查看答案和解析>>

    科目：初中数学 来源：北京市2016-2017学年七年级（下）期中数学试卷 题型：解答题

    如图，四边形ABCD中，∠A=∠C=90°，BE平分∠ABC，DF平分∠ADC，则BE与DF有何位置关系？试说明理由．

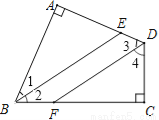
    BE∥DF 【解析】试题分析：根据四边形的内角和定理和∠A=∠C=90°，得∠ABC+∠ADC=180°；根据角平分线定义、等角的余角相等易证明和BE与DF两条直线有关的一对同位角相等，从而证明两条直线平行． 试题解析：BE∥DF．理由如下： ∵∠A=∠C=90°（已知）， ∴∠ABC+∠ADC=180°（四边形的内角和等于360°）． ∵BE平分∠ABC，DF平分∠...

    查看答案和解析>>

    同步练习册答案