
科目:初中数学 来源:福建省2017-2018学年九年级数学上学期期末检测试卷 题型:单选题
一元二次方程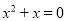 的根是( )
的根是( )
A. x1=0,x2=1 B. x1=0,x2=-1 C. x1=1,x2=-1 D. x1=x2=-1
B 【解析】试题解析: 或 故选B.查看答案和解析>>
科目:初中数学 来源:浙江省2017-2018学年八年级上学期第二次学情检测数学试卷 题型:填空题
命题“同位角相等,两直线平行”的逆命题是: .
两直线平行,同位角相等. 【解析】试题分析:把一个命题的题设和结论互换就得到它的逆命题. 【解析】 命题:“同位角相等,两直线平行.”的题设是“同位角相等”,结论是“两直线平行”. 所以它的逆命题是“两直线平行,同位角相等.” 故答案为:“两直线平行,同位角相等”.查看答案和解析>>
科目:初中数学 来源:江苏省南通市2018届九年级上学期第三次月考数学试卷 题型:解答题
如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,求该船航行的距离(即AB的长).
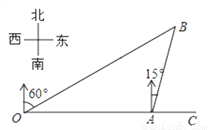
查看答案和解析>>
科目:初中数学 来源:江苏省南通市2018届九年级上学期第三次月考数学试卷 题型:填空题
如图,在△ABC中,AB=AC=6,∠A=2∠BDC, BD交AC边于点E,且AE=4,则BE·DE=____________.
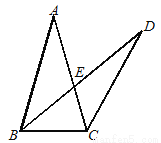
查看答案和解析>>
科目:初中数学 来源:江苏省南通市2018届九年级上学期第三次月考数学试卷 题型:单选题
在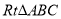 中,
中, 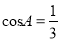 ,那么
,那么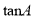 的值是( )
的值是( )
A. 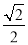 B.
B. 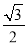 C.
C. 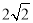 D.
D. 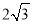
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市2017-2018学年七年级上学期中考试数学试卷 题型:解答题
【阅读理解】
若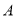 ,
, 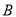 ,
, 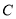 为数轴上三点,若点
为数轴上三点,若点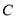 到
到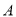 的距离是点
的距离是点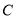 到
到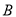 的距离的
的距离的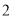 倍,我们就称点
倍,我们就称点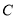 是
是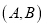 的优点.例如,如图①,点
的优点.例如,如图①,点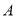 表示的数为
表示的数为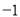 ,点
,点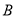 表示的数为
表示的数为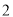 .表示数
.表示数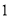 的点
的点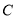 到点
到点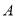 的距离是
的距离是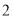 ,到点
,到点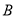 的距离是
的距离是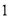 ,那么点
,那么点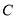 是
是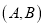 的优点;又如,表示
的优点;又如,表示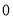 的点
的点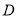 到点
到点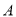 的距离是
的距离是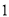 ,到点
,到点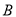 的距离是
的距离是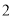 ,那么但点
,那么但点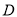 是
是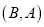 的好点.
的好点.
【知识运用】
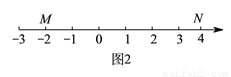
如图②,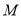 、
、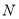 为数轴上两点,点
为数轴上两点,点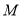 所表示的数为
所表示的数为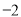 ,点
,点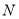 所表示的数为
所表示的数为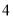 .
.
(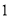 )数__________所表示的点是
)数__________所表示的点是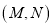 的优点.
的优点.
(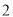 )如图③,
)如图③,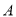 ,
, 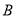 为数轴上两点,点
为数轴上两点,点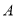 所表示的数为
所表示的数为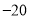 ,点
,点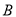 所表示的数为
所表示的数为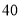 .现有一只电子蚂蚁
.现有一只电子蚂蚁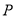 从点
从点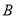 出发,以
出发,以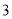 个单位每秒的速度向左运动,到达点
个单位每秒的速度向左运动,到达点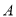 停止.当
停止.当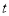 为何值时,
为何值时, 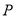 、
、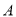 和
和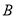 中恰有一个点为其余两点的好点?(请直接写出答案)
中恰有一个点为其余两点的好点?(请直接写出答案)
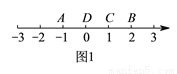
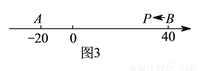
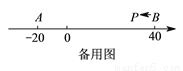
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市2017-2018学年七年级上学期中考试数学试卷 题型:单选题
如图,数轴上有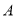 ,
, 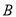 ,
, 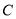 ,
, 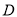 四个整数点(即各点均表示整数),且
四个整数点(即各点均表示整数),且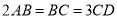 .若
.若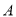 ,
, 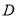 两点所表示的数分别是
两点所表示的数分别是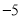 和
和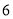 ,则线段
,则线段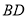 的中点所表示的数是( ).
的中点所表示的数是( ).

A. 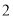 B.
B. 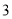 C.
C. 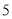 D.
D. 
查看答案和解析>>
科目:初中数学 来源:四川省自贡市2017-2018学年上学期期末考试八年级数学试卷 题型:解答题
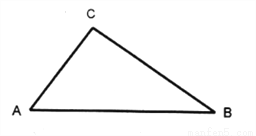
如图,已知?ABC.
(1)用直尺和圆规作出?ABC的角平分线CD;(不写作法,但保留作图痕迹)
(2)过点D画出?ACD的高DE和?BCD的高DF;
(3)量出DE,DF的长度,你有怎样的发现?并把你的发现用文字语言表达出来.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com