
�۲����и�ʽ��
13��12
13��23��32
13��23��33��62
13��23��33��43��102
��
����13��23��33������103��_____.
552 �����������������13=12 13+23=��1+2��2=32 13+23+33=��1+2+3��2=62 13+23+33+43=��1+2+3+4��2=102 13+23+33+��+103=��1+2+3��+10��2=552�� �������� �������ݿɷ���������Ϊ��1��ʼ������n������������=��1+2+��+n��2 ����13+23+33+��+103=��1+...
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���㶫ʡ�����з�خ��2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
һ���鷨��ȤС����2��Ů����3����������Ҫ����5��ѧ����ѡ��2�˴���С��μӱ�������һ��һŮ��ѡ�ĸ�����____��
����������������� �б��ã� ��1 ��2 ��3 Ů1 Ů2 ��1 ��2��1 ��3��1 Ů1��1 Ů2��1 ��2 ��1��2 ��3��2 Ů1��2 Ů2��2 ��3 ��1��3 ��2��3 Ů1��3 Ů2��3 Ů1 ��1Ů1 ��...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ����꼶���ϣ�������ѧģ���Ծ� ���ͣ������
������ֵ��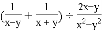 ������x��y����|x-2|��(2x��y��3)2��0��
������x��y����|x-2|��(2x��y��3)2��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ����꼶���ϣ�������ѧģ���Ծ� ���ͣ���ѡ��
��ͼ���������ڲ�������Ĺ����������A��B��ľ��룬���ӳ�AO��C��ʹCO=AO���ӳ�BO��D��ʹDO=BO�����COD�ա�AOB���Ӷ�ͨ������CD�Ϳɲ��A��B��ľ��룬��ȫ�ȵĸ����ǣ�������
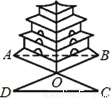
A. SAS B. ASA C. AAS D. SSS
A ���������ڡ�COD�͡�AOB�У� �� ���COD�ա�AOB��SAS���� ��ѡA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������������2017-2018ѧ�����꼶�ϲ���ѧ��ĩ�Ծ� ���ͣ������
ij�̳��Խ���������������A��B��C����Ʒ�����ӵ����������ͳ�ƣ�������ͼ1��ͼ2��ʾ��ͳ��ͼ������ͼ����Ϣ����������⣺
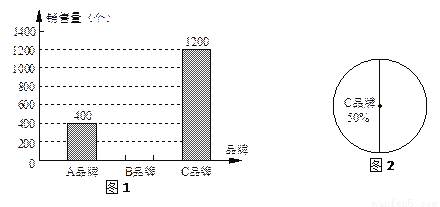
��1����һ��Ʒ�����ӵ����������
��2����ȫͼ1�е�����ͳ��ͼ��
��3��д��AƷ��������ͼ2������Ӧ��Բ�ĽǵĶ�����
��1��CƷ�֣���2����ȫͼ�μ���������3��60�� �������������������1��������ͳ��ͼ�еó�CƷ�Ƶ����������Ϊ50%�� ��2����������=1200��50%=2400����BƷ�Ƶ�������=2400-1200-400=800������ȫͼ�μ��ɣ� ��3��AƷ��������ͼ������Ӧ��Բ�ĽǵĶ���=360�����400��2400��=60�㣻 ��������� ��1��CƷ��. ��2��1200��5...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������������2017-2018ѧ�����꼶�ϲ���ѧ��ĩ�Ծ� ���ͣ������
2016�꣬�ҹ�����1 240���˸��ƶ����Ϊ������ƶ����������Խ���ף���1 240���ÿ�ѧ��������ʾΪa��10n����ʽ����a��ֵ��___��
1.24 ����������ѧ�������ı�ʾ��ʽΪa��10n����ʽ������1��|a|��10��nΪ������ n��ֵ�����������������λ����1������1 240��=12 400 000= 1.24��107������a=1.24.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������������2017-2018ѧ�����꼶�ϲ���ѧ��ĩ�Ծ� ���ͣ���ѡ��
����������ȷ���ǣ�������
A. 4x+3y=7xy B. 3a2��2a2=1 C. 3x2y��3yx2=0 D. 2a3+4a3=6a6
C �����������������A.����ͬ������ܺϲ�.�ʴ���. B. �ʴ���. C.��ȷ. D. �ʴ���. ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��������2017-2018ѧ����꼶��ѧ����ĩ���������ѧ�Ծ� ���ͣ������
��֪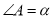 ������
������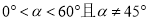 �����ڡ�A�������ϸ���ȡһ��ֱ��ΪM��N�������õ�ֱ���һ��ֱ�ߣ���ʹ�ø�ֱ���������ڵıн�ҲΪ
�����ڡ�A�������ϸ���ȡһ��ֱ��ΪM��N�������õ�ֱ���һ��ֱ�ߣ���ʹ�ø�ֱ���������ڵıн�ҲΪ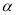 ��������ֱ�߽��ڵ�O�����MON��______________________��
��������ֱ�߽��ڵ�O�����MON��______________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡʮ���е�������2018����꼶���ϣ�������ѧ�Ծ� ���ͣ������
��֪������y=x2-(m+1)x+m��
��1����֤����������x��һ���н��㣻
��2������������x�ύ��A(x1,0����B��x2,0�����㣬x1��0��x2,��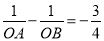 ,��m��ֵ.
,��m��ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com