
已知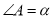 (其中
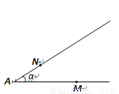
(其中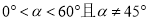 ),在∠A两条边上各任取一点分别记为M、N,并过该点分别引一条直线,并使得该直线与其所在的边夹角也为
),在∠A两条边上各任取一点分别记为M、N,并过该点分别引一条直线,并使得该直线与其所在的边夹角也为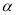 ,设两条直线交于点O,则∠MON=______________________.
,设两条直线交于点O,则∠MON=______________________.
科目:初中数学 来源:海南省2017-2018学年度第一学期七年级数学期中试卷 题型:填空题
若关于x的方程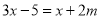 的解为
的解为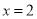 ,则m的值为___________.
,则m的值为___________.
查看答案和解析>>
科目:初中数学 来源:湖南邵阳市区2017-2018学年七年级上册数学期末试卷 题型:填空题
观察下列各式:
13=12
13+23=32
13+23+33=62
13+23+33+43=102
…
猜想13+23+33+…+103=_____.
552 【解析】试题分析:13=12 13+23=(1+2)2=32 13+23+33=(1+2+3)2=62 13+23+33+43=(1+2+3+4)2=102 13+23+33+…+103=(1+2+3…+10)2=552. 【解析】 根据数据可分析出规律为从1开始,连续n个数的立方和=(1+2+…+n)2 所以13+23+33+…+103=(1+...查看答案和解析>>
科目:初中数学 来源:湖南邵阳市区2017-2018学年七年级上册数学期末试卷 题型:单选题
下列说法中正确的是( )
A. 0既不是整数也不是分数 B. 整数和分数统称有理数
C. 一个数的绝对值一定是正数 D. 绝对值等于本身的数是0和1
B 【解析】试题解析:A.0是整数.故错误. B.正确. C.0的绝对值是0.故错误. D.非负数的绝对值都等于它本身.故错误. 故选B.查看答案和解析>>
科目:初中数学 来源:江西省景德镇市2017-2018学年八年级上学期期末质量检测数学试卷 题型:解答题
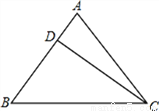
已知等腰三角形ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm.
(1)求证:CD⊥AB;
(2)求该三角形的腰的长度.
查看答案和解析>>
科目:初中数学 来源:江西省景德镇市2017-2018学年八年级上学期期末质量检测数学试卷 题型:填空题
点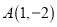 在第__________象限;
在第__________象限;
查看答案和解析>>
科目:初中数学 来源:宁夏中卫市2018届九年级(上)期中数学试卷 题型:解答题
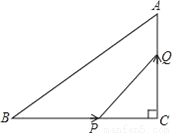
如图,△ABC中,∠C=90°,AC=3cm,BC=4cm,动点P从点B出发以2cm/s的速度向点C移动,同时动点Q从C出发以1cm/s的速度向点A移动,设它们的运动时间为t.
(1)t为何值时,△CPQ的面积等于△ABC面积的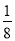 ?
?
(2)运动几秒时,△CPQ与△CBA相似?
(3)在运动过程中,PQ的长度能否为1cm?试说明理由.
查看答案和解析>>
科目:初中数学 来源:宁夏中卫市2018届九年级(上)期中数学试卷 题型:单选题
已知一元二次方程mx2+n=0(m≠0),若方程有解,则必须( )
A. n=0 B. mn同号 C. n是m的整数倍 D. mn异号
D 【解析】试题解析: 异号, 故选D.查看答案和解析>>
科目:初中数学 来源:浙江省杭州市白马湖2017-2018学年八年级上学期期中数学试卷(含解析) 题型:填空题
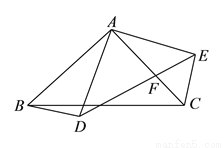
如图 与
与 都是以
都是以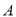 为直角顶点的等腰直角三角形,
为直角顶点的等腰直角三角形, 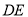 交
交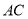 于点
于点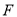 ,若
,若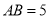 ,
, 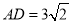 ,当
,当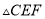 是直角三角形时,则
是直角三角形时,则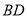 的长为__________.
的长为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com