练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若规定两数a、b通过“※”运算，得到4ab，即a※b=4ab，例如2※6=4×2×6=48

    （1）求3※5的值；

    （2）求x※x+2※x-2※4=0中x的值；

    （3）若无论x是什么数，总有a※x=x，求a的值．

    (1) x1=2，x2=-4;(2) x1=2，x2=-4;(3) 【解析】试题分析：要注意a※b=4ab新定义的运算方法，把已知数按照运算法则代入即可求值，后两问将数值代入后得到了两个方程，解方程即可． 试题解析：【解析】 （1）∵a※b=4ab，∴3※5=4×3×5=60； （2）由x※x+2※x﹣2※4=0得，4x2+8x﹣32=0，即x2+2x﹣8=0，∴x1=2，x2...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：四川省宜宾市2017-2018学年上学期期末教学质量监测八年级数学试卷 题型：解答题

    2017年4月23日是 “世界读书日”，宜宾市某中学举行“多读书，读好书”活动，对学生的课外读书时间进行了随机问卷调查，用调查结果绘制了图1、图2两幅统计图（均不完整），请根据统计图解答以下问题：

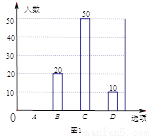
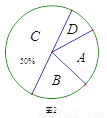
    (1)本次接受问卷调查的学生共有________人，在扇形统计图中“D”选项所占的百分比为________；

    (2)扇形统计图中，“B”选项所对应扇形圆心角为________度；

    (3)请补全条形统计图；

    (4)若该校共有1200名学生，则该校学生课外读书时间在“A”选项的约有_____人.

    100 10% 72 240 【解析】试题分析： （1）由两幅统计图可知，B选项有50人，占被调查总数的50%，由此即可计算接受调查的学生数为100人，结合D选项有10人可计算出在扇形统计图中D选项所占的百分比为10%； （2）结合图形统计图中的信息和（1）中的计算结果，可得扇形统计图中B选项所对应的圆心角为：360°×20%=72°； （3）由（1）中所得接受调查的总人数...

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学九年级上册第二章第三节《用公式法求解一元一次方程》课时练习 题型：单选题

    用公式法解-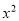+3x=1时，先求出a、b、c的值，则a、b、c依次为（　　）

    A. -1，3，-1 B. 1，-3，-1 C. -1，-3，-1 D. 1，-3，1

    A 【解析】【解析】 -+3x=1，-+3x-1=0，∴a=-1，b=3，c=-1．故选A．

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学九年级上册第一章特殊平行四边形第二节《矩形的性质与判定》课时练习 题型：单选题

    矩形的对角线所成的角之一是65°，则对角线与各边所成的角度是（　　）

    A. 57.5° B. 32.5° C. 57.5°，23.5° D. 57.5°，32.5°

    D 【解析】【解析】 ∵四边形ABCD是矩形，∴∠ABC=90°，AD∥BC，AB∥CD，AC=BD，AO=OC，OB=OD，∴OB=OA=OC=OD，∠OAB=∠OCD，∠DAO=∠OCB，∴∠OAD=∠ODA，∠OCB=∠OBC，∠ODC=∠OCD，∠OAB=∠OBA=×（180°﹣∠AOB）=×（180°﹣65°）=57.5°，∵∠ABC=90°，∴∠ACB=90°﹣57.5°=32...

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学九年级上册第一章特殊平行四边形第二节《矩形的性质与判定》课时练习 题型：单选题

    如图，矩形ABCD的两条对角线交于点O，若∠AOD=120°，AB=6，则AC等于（ ）

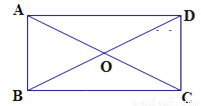
    A. 8 B. 10 C. 12 D. 18

    C 【解析】试题分析：根据∠AOD=120°可得∠AOB=60°，根据矩形的性质可得AO=BO，则△AOB是正三角形，则AO=AB=6，则AC=2AO=12．

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级数学（上）第二章《一元二次方程》同步测试：2.4用因式分解法求解一元二次方程 题型：填空题

    若方程x2-7x+12=0的两根恰好是一个直角三角形两条直角边的长，则这个直角三角形的斜边长是_______________．

    5 【解析】【解析】 解方程x2﹣7x+12=0，解得x=3，x=4；由勾股定理得：斜边长==5．故答案为：5．

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级数学（上）第二章《一元二次方程》同步测试：2.4用因式分解法求解一元二次方程 题型：填空题

    方程（x-3）2=x-3的根是_________________．

    x1=3，x2=4 【解析】【解析】 （x﹣3）2=x﹣3，（x﹣3）2﹣（x﹣3）=0，（x﹣3）（x﹣3﹣1）=0，∴x1=3，x2=4．故答案为：x1=3，x2=4．

    查看答案和解析>>

    科目：初中数学 来源：初三数学第一学期1.1.1菱形的定义与性质 同步练习 题型：填空题

    如图，在边长为2的菱形ABCD中，∠B=45°，AE为BC边上的高，将△ABE沿AE所在直线翻折得△AB1E，则△AB1E与四边形AECD重叠部分的面积是_______．

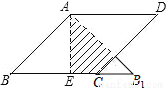
    【解析】【解析】 如图，设CD与AB1交于点O，∵在边长为2的菱形ABCD中，∠B=45°，AE为BC边上的高，∴AE=，由折叠易得△ABB1为等腰直角三角形，∴S△ABB1=BA•AB1=2，S△ABE=1，∴CB1=2BE﹣BC=，∵AB∥CD，∴∠OCB1=∠B=45°，又由折叠的性质知，∠B1=∠B=45°，∴CO=OB1=，∴S△COB1=OC•OB1=，∴重叠部分的面积为：2﹣1﹣（...

    查看答案和解析>>

    科目：初中数学 来源：广东省广州市天河区2017-2018学年七年级上学期期末考试数学试卷 题型：解答题

    如图，已知线段AB的长度是xcm，线段BC的长度比线段AB的长度的2倍多1cm，线段AD的长度比线段BC长度的2倍少1cm，求线段BC，AD和CD的长.

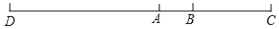
    BC=（2x+1）cm，AD=（4x+1）cm，CD=（7x+2）cm 【解析】试题分析：由AB=xcm得出BC=（2x+1）cm，进而得出AD=2（2x+1）－1=（4x+1）cm，则CD=AD+AB+BC=（7x+2）cm. 试题解析： 【解析】 BC=（2x+1）cm ， AD=2（2x+1）－1=（4x+1）cm， CD= AD+AB+BC=（2x+1）+x...

    查看答案和解析>>

    同步练习册答案