练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

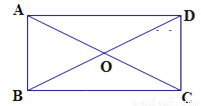
    如图，矩形ABCD的两条对角线交于点O，若∠AOD=120°，AB=6，则AC等于（ ）

    A. 8 B. 10 C. 12 D. 18

    C 【解析】试题分析：根据∠AOD=120°可得∠AOB=60°，根据矩形的性质可得AO=BO，则△AOB是正三角形，则AO=AB=6，则AC=2AO=12．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版八年级数学上册 第七章 平行线的证明 单元测试 题型：单选题

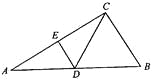
    如图,△ABC中，∠ACB=90°, ∠A=30°AC的中垂线交AC于E.交AB于D，则图中60°的角共有 ( )

    A. 6个 B. 5个 C. 4个 D. 3个

    B 【解析】 ∠B=∠DCB=∠BDC=∠CDE=∠ADE=60° 共5个角为60° 故选B

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学九年级上册第二章第三节《用公式法求解一元一次方程》课时练习 题型：单选题

    方程x2-3x+2=0的最小一个根的倒数是（　　）

    A. 1 B. 2 C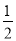 D．4

    A 【解析】【解析】 x2﹣3x+2=0，（x﹣1）（x﹣2）=0，x﹣1=0或x﹣2=0，x1=1或x2=2，所以方程x2﹣3x+2=0的最小一个根的倒数是1，故选A．

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学九年级上册第一章特殊平行四边形第二节《矩形的性质与判定》课时练习 题型：填空题

    平行四边形ABCD的对角线相交于点O，分别添加下列条件：①∠ABC=90°；②AC⊥BD；③AB=BC；④AC平分∠BAD；⑤AO=DO．使得四边形ABCD是矩形的条件有________

    ①⑤ 【解析】【解析】 要使得平行四边形ABCD为矩形添加：①∠ABC=90°；⑤AO=DO2个即可；故答案为：①⑤．

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学九年级上册第一章特殊平行四边形第二节《矩形的性质与判定》课时练习 题型：单选题

    矩形具有而菱形不具有的性质是（　　）

    A. 对角线相等 B. 两组对边分别平行

    C. 对角线互相平分 D. 两组对角分别相等

    A 【解析】【解析】 ∵矩形具有的性质是：对角线相等且互相平分，两组对边分别平行，两组对角分别相等；菱形具有的性质是：两组对边分别平行，对角线互相平分，两组对角分别相等； ∴矩形具有而菱形不具有的性质是：对角线相等． 故选A．

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级数学（上）第二章《一元二次方程》同步测试：2.4用因式分解法求解一元二次方程 题型：解答题

    若规定两数a、b通过“※”运算，得到4ab，即a※b=4ab，例如2※6=4×2×6=48

    （1）求3※5的值；

    （2）求x※x+2※x-2※4=0中x的值；

    （3）若无论x是什么数，总有a※x=x，求a的值．

    (1) x1=2，x2=-4;(2) x1=2，x2=-4;(3) 【解析】试题分析：要注意a※b=4ab新定义的运算方法，把已知数按照运算法则代入即可求值，后两问将数值代入后得到了两个方程，解方程即可． 试题解析：【解析】 （1）∵a※b=4ab，∴3※5=4×3×5=60； （2）由x※x+2※x﹣2※4=0得，4x2+8x﹣32=0，即x2+2x﹣8=0，∴x1=2，x2...

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级数学（上）第二章《一元二次方程》同步测试：2.4用因式分解法求解一元二次方程 题型：填空题

    已知（x2+y2）（x2+y2﹣1）=12，则x2+y2的值是__________．

    4 【解析】试题分析：设x2＋y2=m，方程（x2＋y2）（x2＋y2－1）－12=0可化为m（m-1）-12=0，解得，又因x2＋y2＞0，所以x2＋y2=4．

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级数学（上）第二章《一元二次方程》同步测试：2.4用因式分解法求解一元二次方程 题型：单选题

    方程x2+x-12=0的两个根为（　　）

    A. x1=-2，x2=6 B. x1=-6，x2=2 C. x1=-3，x2=4 D. x1=-4，x2=3

    D 【解析】试题分析：将x2+x﹣12分解因式成（x+4）（x﹣3），解x+4=0或x﹣3=0即可得出结论． x2+x﹣12=（x+4）（x﹣3）=0， 则x+4=0，或x﹣3=0， 解得：x1=﹣4，x2=3．

    查看答案和解析>>

    科目：初中数学 来源：广东省广州市天河区2017-2018学年七年级上学期期末考试数学试卷 题型：解答题

    如图的长方形MNPQ是州某市民健身广场的平面示意图，它是由6个正方形拼成的(分别用A，B，C，D，E，F六个字母表示).已知中间最小的正方形A的边长是1米，设正方形C的边长是x米.

    （1）请用含x的代数式分别表示出正方形EF和B的边长；

    （2）观察图形的特点，找出两个等量关系，分别用两种方法列方程求出x的值；

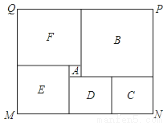
    （3）现沿着长方形广场的四条边铺设下水管道，若甲，乙两个工程队单独铺设分别需要10天和15天完成，如果两队从M处开始，分别沿两个不同方向同时施工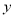天后，因甲队另有任务，余下的工程由乙队单独施工10天完成，求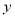的值.

    （1）E的边长=（x+1）米，F的边长为=x+1+1=（x+2）米，B的边长为=x+2+1=（x+3）米 （2）x=4；（3）甲乙同时施工的天数为2天. 【解析】试题分析：（1）因为C的边长是x米，所以D的边长也是x米，又因为A的边长是1米，所以E的边长=（x+1）米，F的边长为=x+1+1=（x+2）米，B的边长为=x+2+1=（x+3）米；（2）①PQ=MN，PQ=F的边长+B的边...

    查看答案和解析>>

    同步练习册答案