
已知直角∠AOB,以O为顶点,在∠AOB的内部画出100条射线,则以OA、OB及这些射线为边的锐角共有多少个?若以O为项点,在∠AOB的内部画出几条射线(n≥1的自然数),则OA、OB以及这些射线为边的锐角共有多少个?

1条射线 1+1=2(个锐角),
2条射线 2+2+1=5(个锐角),
3条射线 3+3+2+1=9(个锐角),
4条射线 4+4+3+2+1=14(个锐角),
……
100条射线 100+100+99+98+…+3+2+1
=100+![]()
=100+5 050
=5 150(个锐角),
n条射线 n+n+(n-1)+(n-2)+…+3+2+1
=n+![]()
=![]() (个锐角).
(个锐角).
【点评】数锐角的个数与数线段的条数一样,以OA为始边,另一条射线为角的终边依次去数,这样可不遗漏不重复地将要数的锐角个数数准确.注意∠AOB是直角,故这个角不在计数的范围内.
若题目改成:已知∠AOB,以O为顶点,在∠AOB的内部画出n条射线,n为非零自然数,以OA、OB以及这些射线为边的角共有多少个?
答案是:共有![]() 个角.
个角.


 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
科目:初中数学 来源: 题型:
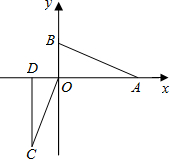 先将Rt△AOB绕原点O按顺时针方向旋转90°后,再沿x轴负方向平移1个单位长度得到△CDO.
先将Rt△AOB绕原点O按顺时针方向旋转90°后,再沿x轴负方向平移1个单位长度得到△CDO.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:数学教研室 题型:044
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com