
��ͼ1���ڡ�ABC�У���B��90�㣬��C��30�㣬��D��C���������CA������2����λÿ����ٶ����յ�A�˶���ͬʱ��E�ӵ�A������AB������1����λÿ����ٶ����յ�B�˶������D��E���˶�ʱ��Ϊt�룬DF��BC��F
��1����֤��AE��DF��
��2����ͼ2������EF��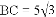
���Ƿ����t��ʹ���ı���AEFDΪ���Σ������ڣ����t��ֵ���������ڣ���˵������
������DE������DEF��ֱ��������ʱ����t��ֵ
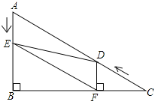
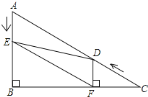

ͼ1 ͼ2 ����ͼ ����ͼ

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ2018����꼶��ѧ�ڵڶ����¿���ѧ�Ծ� ���ͣ������
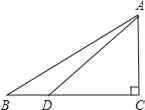
��ͼ����Rt��ABC�У���C��90�㣬��D��BC���ϣ���ADC��45�㣬BD��2��tanB�� .
.
(1)��AC��AB�ij���
(2)��sin��BAD��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���������DZ������н�������2018����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ���ѡ��
��ͼ��ʾ����
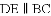
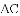
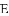
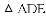
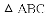
A. 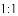
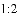
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ�ij���2018���п���ѧ�Ծ� ���ͣ���ѡ��
�����Ǵ�Ⱦ����ļ��ڣ�����Ԥ����Ⱦ����ѧУ�߶����ӵ�һ�����Ϊ�ˣ�ijУ��ѧ�������ȡ����ҩ���������.�ڶ�ij������������Ĺ����У��Ⱦ���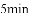
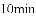
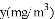 ��ҩ���ڿ����еij���ʱ��
��ҩ���ڿ����еij���ʱ��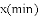
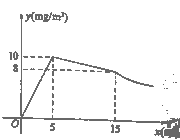
A. ����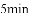
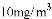
B. ���ڿ����еĺ�ҩ��������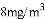 �ij���ʱ��ﵽ��
�ij���ʱ��ﵽ��
C. �����ڿ����еĺ�ҩ��������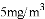 �ҳ���ʱ�䲻����35���ӣ�������Чɱ��ij�ִ�Ⱦ����.�˴�������ȫ��Ч
�ҳ���ʱ�䲻����35���ӣ�������Чɱ��ij�ִ�Ⱦ����.�˴�������ȫ��Ч
D. �����ڿ����еĺ�ҩ������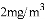 ʱ����������ǰ�ȫ�ģ����Դ����ڿ����еĺ�ҩ���ﵽ
ʱ����������ǰ�ȫ�ģ����Դ����ڿ����еĺ�ҩ���ﵽ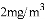 ��ʼ���辭��
��ʼ���辭��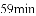
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ�ij���2018���п���ѧ�Ծ� ���ͣ���ѡ��
���м��������ǣ�������
A. a2��a0•a2=a4 B. a2�£�a0•a2��=1
C. ����1.5��8�£���1.5��7=��1.5 D. ��1.58�£���1.5��7=��1.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018����꼶��ѧ����ĩ��ѧ��ǰ���Ծ���һ��(��Χ������+����+ƽ���ı���) ���ͣ������
�����и���ʽ��ʽ�ֽ�
��1��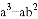 �� ��2��
�� ��2��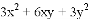
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018����꼶��ѧ����ĩ��ѧ��ǰ���Ծ���һ��(��Χ������+����+ƽ���ı���) ���ͣ������
ƽ���ı��ε��ܳ�����56 cm�����ڱ߳��ı�Ϊ3��1����ô���ƽ���ı��νϳ��ı߳�Ϊ_______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ������2018���п�ȫ��ģ�����ѧ�Ծ� ���ͣ������
ģ�ͽ��ܣ���ϣ����һ�������ġ������������⡱�������������£���ϣ��һλ������ÿ�춼ҪѲ��Ӱ����������ӪA��B����������ȥAӪ���ٵ��ӱ�������֮����ȥBӪ����ͼ�٣���ʱ���룬��ô�߲���ʹÿ���·��֮������أ�
����ѧ�Һ���������ԳƵķ�������Ľ����������.
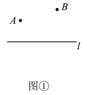
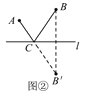
��ͼ�ڣ���B����ֱ��l�ĶԳƵ�B�䣬����AB����ֱ��l���ڵ�C����C���������λ�ã�
���������е��Ķ���Ӧ�õĹ����У���ɽ��
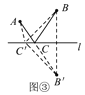
��1�����ɣ���ͼ�ۣ���ֱ��l����ȡ��һ��C�䣬����AC�䣬BC�䣬B��C�䣬
��ֱ��l�ǵ�B��B��ĶԳ��ᣬ��C��C����l�ϣ�
��CB=_______��C��B=_______.
��AC+CB=AC+CB��=_______��
�ڡ�AC��B���У���AB�䣼AC��+C��B�䣬��AC+CB��AC��+C��B�䣬��AC+CB��С.
�����
������ʵ����������ԳƱ任��˼�룬��A��B��ֱ�ߵ�ͬ������ת��Ϊ��ֱ�ߵ����࣬�Ӷ������á�����֮���߶���̡�����ת��Ϊ������������֮�ʹ��ڵ����ߡ���������Խ��������CΪAB����l�Ľ��㣬��A��C��B�����㹲�ߣ���
���������չΪ����ֱ����һ������ֱ����������ľ���͵���Сֵ���������ѧģ�ͣ�
��2��ģ��Ӧ��
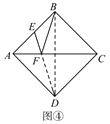
����ͼ �ܣ�������ABCD�ı߳�Ϊ2��EΪAB���е㣬F��AC��һ���㣬��EF+FB����Сֵ.
���������⣬���Խ��������ģ�ͣ��������εĶԳ��Կ�֪��B��D����ֱ��AC�Գƣ�����ED��AC��F����EF+FB����Сֵ�����߶�DE�ij��ȣ�EF+FB����Сֵ��_______��
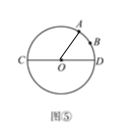
����ͼ�ݣ���֪��O��ֱ��CDΪ4����AOD�Ķ���Ϊ60�㣬��B�ǻ�AD���е㣬��ֱ��CD����һ��P��ʹBP+AP��ֵ��С����BP+AP����Сֵ��_______��
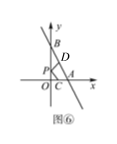
����ͼ�ޣ�һ�κ���y=-2x+4��ͼ����x��y��ֱ���A��B���㣬��OΪ����ԭ�㣬��C���D�ֱ�Ϊ�߶�OA��AB���е㣬��PΪOB��һ���㣬��PC+PD����Сֵ����д��ȡ����СֵʱP�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018���㽭ʡ��������У������ѧ�Ծ� ���ͣ������
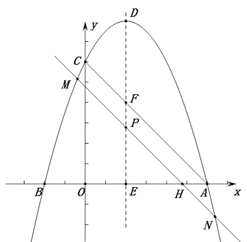
��ͼ��������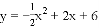 ��x����A��B���㣨��A�ڵ�B���Ҳࣩ����y���ڵ�
��x����A��B���㣨��A�ڵ�B���Ҳࣩ����y���ڵ�
C������ΪD���Գ���ֱ�x�ᡢAC�ڵ�E��F����P������DE��һ���㣬����P��AC��ƽ����
MN��x���ڵ�H�����������ڵ�M��N����Mλ�ڶԳ������ࣩ.���P��������Ϊt..
��1���������ߵĶԳ��ἰ��A������.
��2������Pλ��EF���е�ʱ�����M������.
��3���� ��P���߶�DE���˶�ʱ����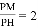 ʱ����t��ֵ.
ʱ����t��ֵ.
�� ��Q����������һ�㣬��P�������˶������У������Ե�C��P��M��QΪ������ı�����ƽ��
�ı���ʱ�����ʱt��ֵ�� ����ֱ��д���𰸣�.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com