
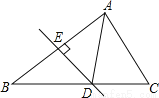
��ͼ������ACD���ܳ�Ϊ7cm��DEΪAB�ߵĴ�ֱƽ���ߣ���AC+BC=_____cm��
 ��һ����ͬ���ɽ�����ϵ�д�
��һ����ͬ���ɽ�����ϵ�д� ������Ӧ���ϵ�д�
������Ӧ���ϵ�д� ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���㽭ʡ������۴������У2017-2018ѧ����꼶�ϲ���ѧ��һ���¿��Ծ� ���ͣ���ѡ��
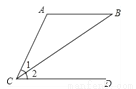
��ͼ��ʾ��������������������AC=AB����AB��CD���ۡ�1=��2������������������ѡ������Ϊ���裬��һ����Ϊ���ۣ������������ĸ���Ϊ��������
A. 0 B. 1 C. 2 D. 3
D �����������еȿ��ܵ������3�֣��ֱ�Ϊ�٢�⇒�ۣ��٢�⇒�ڣ��ڢ�⇒�٣�������������������������У��٢�⇒�ۣ��٢�⇒�ڣ��ڢ�⇒�٣� ��ѡ��D.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ������
Rt��ABC�У�CD��б��AB�ϵĸߣ���B=30�㣬AD=2cm����AB�ij�����_____cm��
8 ����������Rt��ABC�� ��CD��б��AB�ϵĸ� ���ADC=90�� ���ACD=��B=30�㣨ͬ�ǵ������ȣ� ��AD=2cm ��Rt��ACD�У�AC=2AD=4cm ��Rt��ABC�У�AB=2AC=8cm ��AB�ij�����8cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�Ƹ���2017-2018ѧ����꼶���ϣ�������ѧ�� ���ͣ������
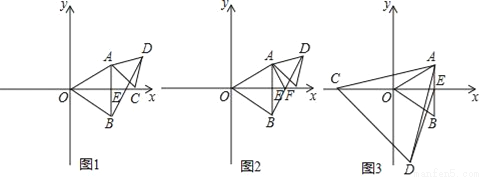
��ͼ��AOB�͡�ACD�ǵȱ������Σ�����AB��x����E�㣮
��1����ͼ����OC=5����BD�ij��ȣ�
��2����BD��x���ڵ�F����֤����OFA=��DFA��
��3����ͼ��������AOB�ı߳�Ϊ4����CΪx����һ���㣬��ACΪ����ֱ��AC�·�������ACD������ED����ED����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�Ƹ���2017-2018ѧ����꼶���ϣ�������ѧ�� ���ͣ������
��ͼ����֪��A��C��B��D��ͬһ��ֱ���ϣ�AC=BD��AM=CN��BM=DN��
��֤����AMB�ա�CND��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�Ƹ���2017-2018ѧ����꼶���ϣ�������ѧ�� ���ͣ���ѡ��
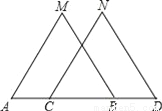
��ͼ��E�ǵȱ�������ABC��AC���ϵĵ㣬��1����2��BE��CD�����ADE����״��( )
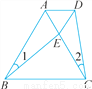
A. һ����������� B. �ȱ������� C. ���ȱ������� D. ����ȷ����״
B �����������������E�ǵȱߡ�ABC��AC���ϵĵ㣬AB=AC������Ϊ��1=��2��BE=CD�����ԣ���AE=AD�� �����ԡ�ADE����״�ǵȱ������Σ���һ������60�ȵĵ����������ǵȱ������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�Ƹ���2017-2018ѧ����꼶���ϣ�������ѧ�� ���ͣ���ѡ��
��ͼ��AB��CD����A=35�㣬��C=75�㣬���E�Ķ���Ϊ��������
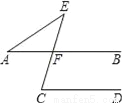
A. 35�� B. 40�� C. 45�� D. 75��
B �������������������AB��CD�� ��ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ��ͷ�г�������Ӣ��2018����꼶��ѧ����ĩ�ʼ���ѧ�Ծ� ���ͣ���ѡ��
��ͼ��������ABCD�ı߳�Ϊ3cm������P��B�������3cm/s���ٶ����ű�BC��CD��DA�˶�������A��ֹͣ�˶�����һ����Qͬʱ��B���������1cm/s���ٶ����ű�BA��A���˶�������A��ֹͣ�˶�����P���˶�ʱ��Ϊx��s������BPQ�����Ϊy��cm2������y����x�ĺ���ͼ���ǣ�������
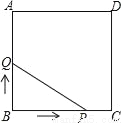
A. 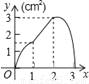 B.
B. 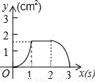 C.
C. 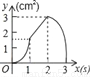 D.
D. 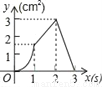
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������2018����꼶���ϣ�������ѧ�Ծ� ���ͣ������
��֪����x�ķ���x2��3x+m=0��
��1����mΪ��ֵʱ��������������ȵ�ʵ������
��2����m=��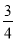 ʱ���̵Ľ⣮
ʱ���̵Ľ⣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com