练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知关于x的方程x2﹣3x+m=0．

    （1）当m为何值时，方程有两个相等的实数根；

    （2）当m=﹣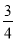时，求方程的解．

    （1）m=；（2）x1=，x2=． 【解析】试题分析： （1）由方程有两个相等的实数根可得出根的判别式△=9﹣4m=0，解之即可得出m的值； （2）将（1）中所求m的值代入原方程，用公式法解方程即可得出结论． 试题解析： （1）∵方程x2﹣3x+m=0有两个相等的实数根， ∴△=（﹣3）2﹣4m=9﹣4m=0， 解得：m=． （2）将m=﹣代入原方程...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：湖北省黄冈市2017-2018学年八年级（上）期中数学试 题型：填空题

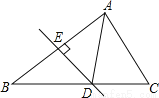
    如图，若△ACD的周长为7cm，DE为AB边的垂直平分线，则AC+BC=_____cm．

    7 【解析】由已知条件，根据垂直平分线的性质得到AD=BD，进行等量代换后可得答案． 【解析】 ∵DE为AB边的垂直平分线 ∴DA=DB ∵△ACD的周长为7cm ∴AD+AC+CD=AC+BC=7． 故填7． 此题主要考查线段的垂直平分线的性质等几何知识；利用垂直平分线的性质后进行线段的等量代换是正确解答本题的关键．

    查看答案和解析>>

    科目：初中数学 来源：江苏省2017-2018学年七年级上学期第二次月考数学试卷 题型：解答题

    某校有住宿生若干人，若每间宿舍住8人，则有5人无处住；若每间宿舍增加1人，则还空30张床位，一共有住校生多少人？

    住校生285人 【解析】试题分析：首先设共有x间宿舍，根据关键语句“每间宿舍住8人，则有5人无处住；若每间宿舍增加1人，则还空35张床位”可得方程8x+5=9x-35，再解方程即可． 试题解析：设共有x间宿舍，由题意得： 8x+5=9x-30， 解得：x=35， 8×35+5=285（人）， 答：一共有住校生285人．

    查看答案和解析>>

    科目：初中数学 来源：江苏省2017-2018学年七年级上学期第二次月考数学试卷 题型：填空题

    某天温度最高是12℃，最低是－7℃，这一天温差是 ℃．

    19． 【解析】试题分析：12-（-7）=19（℃）． 故答案为：19．

    查看答案和解析>>

    科目：初中数学 来源：北京市2018届九年级（上）期中数学试卷 题型：解答题

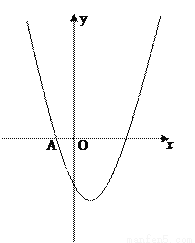
    已知抛物线y=x2+bx﹣3（b是常数）经过点A（﹣1，0）．

    （1）求该抛物线的解析式和顶点坐标；

    （2）P（m，t）为抛物线上的一个动点，P关于原点的对称点为P'．

    ① 当点P' 落在该抛物线上时，求m的值；

    ② 当点P' 落在第二象限内，P'A2取得最小值时，求m的值．

    （1）（1，-4）（2） 【解析】试题分析： （1）把点A（-1，0）代入抛物线y=x2+bx﹣3解得b的值，即可得到抛物线的解析式；把所得解析式配方化为“顶点式”即可得到抛物线的顶点坐标； （2）①由点P的坐标（m，t）可得点P′的坐标为（-m，-t），把两点的坐标分别代入（1）中所求抛物线的解析式可得：t=m2﹣2m﹣3，t=﹣m2﹣2m+3，由此可得m2﹣2m﹣3=﹣m2﹣...

    查看答案和解析>>

    科目：初中数学 来源：北京市2018届九年级（上）期中数学试卷 题型：填空题

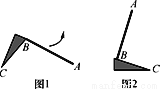
    如图1，教室里有一只倒地的装垃圾的灰斗，BC与地面的夹角为50°，∠C＝25°，小贤同学将它扶起平放在地上(如图2)，则灰斗柄AB绕点C转动的角度为_________．

    105° 【解析】试题分析：灰斗柄AB绕点C转动的角度也就是点B旋转的角度，BC原来与地面夹角为50°，旋转之后与地面夹角为∠C＝25°，所以旋转了180°-25°-50°=105°，所以灰斗柄AB绕点C转动的角度为105°.

    查看答案和解析>>

    科目：初中数学 来源：北京市2018届九年级（上）期中数学试卷 题型：单选题

    如图，在平面直角坐标系中，A点坐标为（﹣4，﹣3），将线段OA绕原点O顺时针旋转90°得到OA′，则点A′的坐标是（　　）

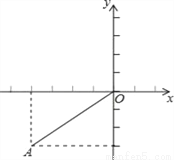
    A. （﹣4，3） B. （﹣3，4） C. （3，﹣4） D. （4，﹣3）

    B 【解析】由题意画出旋转所得线段OA′如下图所示：作AB⊥x轴于点B，作A′C⊥x轴于点C， ∴∠ABO=∠A′CO=90°， 又∵∠A′OA=90°， ∴∠AOB+∠BAO=∠AOB+∠A′OC=90°， ∴∠BAO=∠A′OC， 又∵OA′=OA， ∴△A′OC≌△OAB， ∴A′C=OB，OC=AB， ∵点A的坐标为（-4，-3）， ...

    查看答案和解析>>

    科目：初中数学 来源：辽宁省大连市沙河口区孙家沟九年制学校2018届九年级（上）期中数学试卷 题型：填空题

    实数a，b是关于x的方程2x2+3x+1=0的两根，则点P（a，b）关于原点对称的点Q的坐标为_____．

    （1， ）或（，1） 【解析】2x2+3x+1=0， （2x+1）（x+1）=0， ∴， ∴a=，b=-1或a=-1，b=， ∴点P的坐标为（﹣1， ）或（，﹣1）， ∵点P（a，b）关于原点对称的点Q， ∴点Q的坐标为（1， ）或（ ，1）， 故答案为：（1， ）或（，1）．

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级上册 第十三章 轴对称 13.1 轴对称 同步练习题 题型：单选题

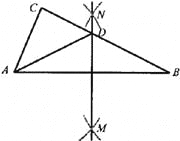
    如图，在△ABC中，分别以点A和点B为圆心，大于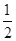AB的长为半径画孤，两弧相交于点M，N，作直线MN，交BC于点D，连接AD．若△ADC的周长为10，AB=7，则△ABC的周长为（ ）。

    A、7 B、14 C、17 D、20

    C. 【解析】根据画法可知MN为AB的垂直平分线，根据线段垂直平分线的性质定理可得AD=BD，又因△ADC的周长为10，可得AC+CD+AD=10，所以AC+CD+BD=10，即AC+BC=10；再由AB＝7，可得△ABC的周长为AC+BC+AB=10+7=17，故选C.

    查看答案和解析>>

    同步练习册答案